Approximation and Simulation of Signal Belonging to the Generalized Weighted Lipschitz Class by ...

Aproximación y Simulación de Señal Perteneciente a la Clase de Lipschitz Generalizada Ponderada ...

Authors

DOI:

https://doi.org/10.24054/bistua.v22i2.2842

Keywords:

Generalized weighted Lipschitz class, Conjugate Fourier series, Holder inequality

Abstract

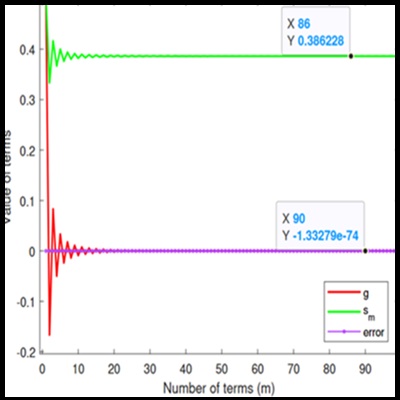
In this study, the well-known Fourier Conjugate series, which is traditionally summable through various individual methods, demonstrates enhanced convergence speed and improved signal approximation when subjected to a product transform. This work aims to establish a novel theorem for approximating signals within a specific function class, utilizing product summability of conjugate Fourier series. Additionally, a range of illustrative examples is provided to validate the proposed summability method and highlight their convergence behavior. The findings are further supported through simulations conducted using MATLAB programming.

Downloads

Download data is not yet available.

Author Biographies

Smita Sonker, Department of Mathematics, National Institute of Technology Kurukshetra, Kurukshetra 136119, India

1. Department of Mathematics, National Institute of Technology Kurukshetra, Kurukshetra 136119, India

2. School of Physical Sciences, Jawaharlal Nehru University, New Delhi 110067, India

Paramjeet Sangwan, Department of Mathematics, National Institute of Technology Kurukshetra, Kurukshetra 136119, India

1. Department of Mathematics, National Institute of Technology Kurukshetra, Kurukshetra 136119, India

 

Bidu Bhusan Jena, Faculty of Science (Mathematics), Sri Sri University, Cuttack 754006, Odisha, India

3. Faculty of Science (Mathematics), Sri Sri University, Cuttack 754006, Odisha, India

Susanta Kumar Paikray, Department of Mathematics, Veer Surendra Sai University of Technology, Burla 768018, Odisha, India

4. Department of Mathematics, Veer Surendra Sai University of Technology, Burla 768018, Odisha, India.

References

Thakur, A. K., Singh, G. K., and Dubey, A. 2022. Approximation of conjugate function related to Lipschitz and weighted class by product summability. Turkish Journal of Computer and Mathematics Education, 13(2), 346-353.

Rathore, A., and Singh, U. 2020. On the degree of approximation of functions in a weighted Lipschitz class by almost matrix summability method. The Journal of Analysis, 28(1), 21-33.

Zygmund, A., 1959. Trigonometric Series. Cambridge University Press.

Borwein, D., 1958. On products of sequences. Journal of the London Mathematical Society, 1(3), 352-357.

Rhoades, B.E., Ozkoklu, K. and Albayrak, I., 2011. On the degree of approximation of functions belonging to a Lipschitz class by Hausdorff means of its Fourier series. Applied Mathematics and Computation, 217(16), 6868-6871.

Hardy, G.H., 1949. Divergent series. Oxford University Press.

Bor, H., 2016. Some new results on absolute Riesz summability of infinite series and Fourier series. Positivity, 20(3), 599-605.

Bor, H., 2015. Some new results on infinite series and Fourier series. Positivity, 19(3), 467-473.

Khan, H.H., 1982. A note on a theorem of Izumi. Comm. Fac. Maths. Ankara, 31, 123-127.

Khan, H. H., 1974. On degree of approximation to a functions belonging to the weighted -class. Aligarh Bull. of Math., 3(4), 83-88.

Nigam, H. K., 2014. Approximation of conjugate function belonging to lipschitzs class by product means. International Journal of Mathematics Research, 15-26.

Rathore, H. L. and Shrivastava, U. K., 2012. Approximation of function belonging to weighted class by product means of its Fourier series. International Journal of Scientific and Research Publications, 6(2).

Qureshi, K., 1982. On the degree of approximation of a function belonging to weighted class. Indian Journal of Pure and Applied Mathematics, 13, 471-475.

Lal, S. and Nigam, H.K., 2001. Degree of approximation of conjugate of a function belonging to Lip class by matrix summability means of conjugate Fourier series. International Journal of Mathematics and Mathematical Sciences, 27(9), 555-563.

Mishra, V. N., Khatri, K. and Mishra, L. N., 2012. Approximation of functions belonging to lipschitzs class byproduct summability of conjugate series of Fourier series. Journal of Inequalities and Applications, 296, 10 p.

Krasniqi, X.Z., 2015. On the Degree of Approximation of Functions Belonging to the Lipschitz Class by product summability Means. Khayyam Journal of Mathematics, 1(2), 243-252.

Deger, U., 2016. On approximation to functions in the weighted class by a new matrix mean. Novi Sad J. Math, 46(1), 1-14.

Singh, U., 2021. On the trigonometric approximation of functions in a weighted Lipschitz class. The Journal of Analysis, 29, 325-335.

Singh, U. and Srivastava, S.K., 2014. Approximation of conjugate of functions belonging to weighted Lipschitz class weighted mean by Hausdorff means of conjugate Fourier series. Journal of Computational and Applied Mathematics, 259, 633-640.

Additional Files

Published

2024-11-02 — Updated on 2024-11-03

Versions

How to Cite

Sonker, S., Sangwan, P., Bhusan Jena, B., & Paikray, S. K. (2024). Approximation and Simulation of Signal Belonging to the Generalized Weighted Lipschitz Class by .: Aproximación y Simulación de Señal Perteneciente a la Clase de Lipschitz Generalizada Ponderada . BISTUA REVISTA DE LA FACULTAD DE CIENCIAS BASICAS, 22(2), 1–8. https://doi.org/10.24054/bistua.v22i2.2842 (Original work published November 2, 2024)

Issue

Vol. 22 No. 2 (2024)

Section

Paper

License

Copyright (c) 2024 © Autores; Licencia Universidad de Pamplona

Creative Commons License

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

© Autores; Licencia Universidad de Pamplona