Diseño e implementación de un sistema de control por retroalimentación de variables de estado para una plataforma Ball and Plate
Design and implementation of a state feedback control system for a Ball and Plate platform
Resumen: El presente artículo mostrará el modelamiento, desarrollo e implementación de un sistema de control LQR PI-Vectorial para una planta electromecánica de dos ejes de libertad, en este caso un “Ball and Plate”. Un controlador LQR PI-vectorial mejora en gran medida los tiempos de respuesta del sistema, permitiendo de esta forma reducir drásticamente sus errores en estado estacionario y provee una rápida respuesta ante perturbaciones externas aplicadas. Esto es óptimo para esta aplicación pues es necesario tener acciones de control rápidas y precisas que harán que la bola se mantenga en la posición de referencia deseada. Se utiliza para la adquisición de datos un sensor piezoeléctrico resistivo de dos ejes, el cual entrega los datos de la posición actual de la bola a un Arduino Mega que tiene como función aplicar los algoritmos implementados de lectura, para posteriormente enviar las acciones de control necesarias a dos servomotores MG995 que se encargan de alterar la posición de la bola mediante el balanceo de esta en los dos ejes de libertad. Se utiliza el software Matlab y su herramienta de simulación Simulink para la obtención de las distintas constantes del controlador y la simulación del lazo de control.
Palabras clave: Control, LQR PI Vectorial, Ball and plate.
Abstract: This article will show the modeling, development and implementation of a PI-Vector LQR control system for an electromechanical plant with two freedom axes, in this case a “Ball and Plate”. A PI-vector LQR controller greatly improves the system's response times, thus allowing its steady-state errors to be drastically reduced and providing a rapid response to applied external disturbances. This is optimal for this application since it is necessary to have quick and precise control actions that will keep the ball in the desired reference position. This will be achieved through the acquisition of data from a two-axis resistive piezoelectric sensor, which delivers the data of the current position of the ball to an Arduino Mega whose function is to apply the implemented algorithms of reading, to later send the control actions to two MG-995 servo motors that will be responsible for altering the position of the ball by balancing it in the two axes of freedom. The Matlab software and its simulation tool Simulink will be used to obtain the different controller constants and simulate the control loop.
Keywords: Control, LQR PI Vectorial, Ball and plate.
1. INTRODUCCIÓN
Un Ball and plate, es una planta de control de dos ejes de libertad que tiene como objetivo, en este caso mantener la posición de una pelota “Ball” sobre una superficie o “Plate” en una referencia deseada, para lograrlo se debe controlar su movimiento en ambos ejes de libertad X, Y.
Para ello se pueden plantear dos sistemas independientes para cada eje, como lo plantean
,
, de este modo si se considera el sistema ideal y lineal se encontrará una función de transferencia que describe el comportamiento del prototipo
,
. Esta función de transferencia en lazo abierto tendrá como característica principal pertenecer a un modelo de segundo orden críticamente amortiguado o también llamado oscilatorio
,
. A partir de esta función de transferencia se obtiene una representación del sistema en espacio de estados
,
, con esta representación en espacio de estados se analizará la controlabilidad de cada sistema lo cual proporciona información sobre la viabilidad en la implementación del controlador
, Finalmente se procede con la implementación del controlador LQR PI Vectorial, el cual permite generar una acción de control más precisa y óptima a diferencia que con los controladores convencionales. Esta técnica de control permite la reducción en gran medida de las oscilaciones presentes en los sistemas, además de aumentar la eficiencia de los mismos
,
.
2. DISEÑO Y CONSTRUCCIÓN
Para el diseño se siguieron los lineamientos propuestos por
,
para el modelamiento del sistema y la obtención de una función de transferencia, para esto primero se analizan las dinámicas de la planta partiendo desde la bola hacia los servomotores. Se tienen en cuenta las siguientes consideraciones:
- La bola está rodando, no deslizándose.
- No hay fricción en el sistema.
- La geometría de la bola es totalmente esférica y homogénea.
A partir de esto se dividió el análisis de los dos ejes X y Y en subsistemas independientes, en la figura 1 se muestran las consideraciones que se tienen por cada eje.
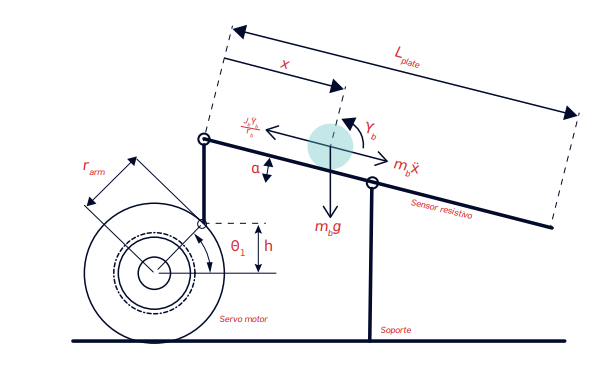
Fig. 1. Diagrama para el análisis de las ecuaciones de movimiento en cada eje de la planta
Fuente: Modelamiento en una dimensión
De esta forma se obtienen dos ecuaciones del movimiento de la bola de cada eje de la siguiente manera:
\[ \frac{{d^2 (x,y)}}{{dt^2 }} = \frac{{m_b \cdot r_b \cdot \left(x \cdot \frac{{d^2 \alpha_{1,2}}}{{dt^2 }} - g \cdot \sin(\alpha_{1,2})\right)}}{{m_b \cdot r_b^2 + I_b }} \hspace{1cm} (1)\]
Como se puede observar en la ecuación (1), se tiene que linealizar la función de transferencia para suprimir el término sinusoidal de la dinámica, para ello se utiliza la aproximación de la serie de Taylor para el seno, la cual indica que el seno de un ángulo puede ser igual al mismo ángulo siempre y cuando este sea cercano a 0, se manejan ángulos de libertad desde -15 hasta 15 grados
. De este modo se puede linealizar para un rango de operación cercano al centro del sensor obteniendo de esta forma la siguiente ecuación de movimiento para el sistema (2):
\[ \frac{{d^2 (x,y)}}{{dt^2}} = \frac{{m_b \cdot r_b^2 \cdot g \cdot \alpha_{1,2}}}{{m_b \cdot r_b^2 + I_b}} \hspace{1cm} (2)\]
A partir de este modelamiento de la propia planta se debe seguir el siguiente esquema en el que se presenta la función de transferencia total del sistema incluyendo la función de transferencia interna de los servomotores.
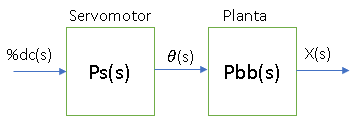
Fig. 2. Diagrama en lazo abierto de la planta Ball and plate
Fuente: elaboración propia.
Para llegar a la función de transferencia, primero se toman las distintas medidas planteadas en la ecuación linealizada del sistema para la obtención de las dos funciones de transferencia, estas medidas se presentan en la tabla 1.
Tabla 1: Características, parámetros y dinámicas del sistema
| Parámetro |
Símbolo |
Valor |
Unidad |
| Resistencia |
R |
4 |
Ω |
| Inductancia |
L |
2.75 |
uH |
| Constante Electromotriz |
Kb |
0.0275 |
V/(rad/s) |
| Constante de torque |
Kp |
0.0275 |
Nm/A |
| Constante de Inercia |
J |
3.2284 |
p(Kg*m*m) |
| Constante de fricción |
B |
3.5077 |
u(Nms/rad) |
| Diámetro de la Bola |
Rb |
0.015 |
m |
| Masa de la bola |
Mb |
0.11 |
Kg |
| Longitud del brazo del motor |
d |
0.017 |
m |
| Distancia a Base de apoyo |
Lp |
0.073 |
m |
Con la información recopilada en la tabla anterior se obtienen finalmente las siguientes funciones de transferencia para ambos ejes.
Eje X:
\[ X(s) = \frac{0.0103}{s^2} \]
Eje Y:
\[ Y(s) = \frac{0.006483}{s^2} \]
En la figura 3 se observa la implementación final del sistema físico:

Fig. 3. Ball and Plate.
Fuente: elaboración propia.
3. CONTROLADOR POR ESPACIO DE ESTADOS.
Para el diseño del controlador primero se tiene que obtener el modelo equivalente en espacio de estados, para ello se parte de las dos funciones de transferencia obtenidas en el capítulo 2, se determina la función de transferencia equivalente en lazo cerrado y se obtendrá un modelo en espacio de estados equivalente para cada eje
.
Para el eje Y:
\[ A_y = \begin{bmatrix} 0 & -0.0065 \\ 1 & 0 \end{bmatrix} \]
\[ B_y = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]
\[ C_y = \begin{bmatrix} 0 & 0.0065 \end{bmatrix} \]
Para el eje X:
\[ A_x = \begin{bmatrix} 0 & -0.0103 \\ 1 & 0 \end{bmatrix} \]
\[ B_x = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]
\[ C_x = \begin{bmatrix} 0 & 0.0065 \end{bmatrix} \]
Para ambos casos se determina una matriz D igual a 0. Para comprobar el funcionamiento de cada eje en lazo abierto se implementan ambos sistemas en Simulink como se aprecia en la figura 4.
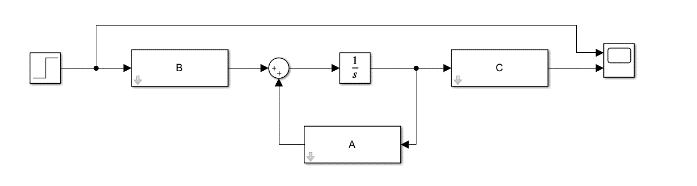
Fig. 4. Representación del sistema en espacio de estados.
Fuente: elaboración propia.
Obteniendo una respuesta oscilante del sistema como se observa en la figura 5, se puede generalizar este comportamiento teniendo en cuenta que ambos subsistemas son críticamente amortiguados.
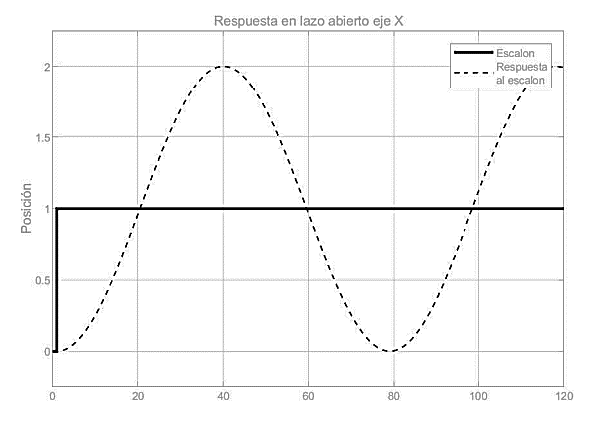
Fig. 5. Respuesta del sistema en lazo abierto.
Fuente: elaboración propia.
Para continuar con el diseño del controlador, ahora se estudia la controlabilidad del sistema, la cual va a decir si es posible implementar un controlador por realimentación de variables de estado para este sistema. Para hallar la controlabilidad se va a determinar el rango de la matriz de controlabilidad, si el rango es N, donde N es el número de variables de estado del sistema
.
\[ \theta_c = [B, (AB)] \hspace{1cm} (3)\]
En (3) se muestra la forma de hallar la matriz de controlabilidad del sistema. de la cual se obtienen las matrices de controlabilidad por cada eje de la siguiente manera:
\[ \theta_{cx} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]
\[ \theta_{cy} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]
Dado que ambas matrices son de rango 2, los dos sistemas son controlables.
Se presenta el diseño un controlador LQR PI Vectorial para cada uno de los ejes. Para ello se obtienen las matrices aumentadas del sistema con el fin de hallar las matrices de ganancias y la ganancia integral del controlador
.
La nueva variable de estado es una variable dependiente del error buscando que el error en estado estacionario sea 0. Para lo cual tendremos las siguientes matrices aumentadas por cada eje.
Eje X:
\[ A_{aux} = \begin{bmatrix} 0 & -0.0103 & 0 \\ 1 & 0 & 1 \\ 0 & 0.0103 & 0 \end{bmatrix} \]
\[ B_{aux} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \]
Eje Y:
\[ A_{auy} = \begin{bmatrix} 0 & -0.0064 & 0 \\ 1 & 0 & 0 \\ 0 & 0.0064 & 0 \end{bmatrix} \]
\[ B_{auy} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \]
Ahora se deben asignar dos polos más a la izquierda del eje imaginario del plano complejo S. Dado que este es un sistema críticamente oscilatorio se sabe que sus polos se encuentran sobre el eje imaginario, por lo consiguiente se pueden asignar cualquier valor negativo, para este caso se asignó la matriz de polos:
\[ Pcl = [-3, -4, -5] \]
Con los polos propuestos se procedió a encontrar el valor de la matriz de ganancias, obteniendo las siguientes ganancias para cada eje:
\[ Gclx = [12, 46.989, 5825] \]
\[ Gcly = [12, 46.999, 9230] \]
Los dos primeros valores de la matriz de ganancia presentada van a pertenecer a la matriz de ganancias de las variables de estado, y el último valor es el valor de la ganancia integral del controlador.
Ahora se procede a montar los controladores LQR Pi Vectorial en Simulink como se muestra en la figura 6:

Fig. 6. Diagrama de bloques de los sistemas con el controlador LQR PI Vectorial implementado.
Fuente: elaboración propia.
Y se obtienen las siguientes respuestas al escalón por cada eje de la siguiente forma:
Eje X:
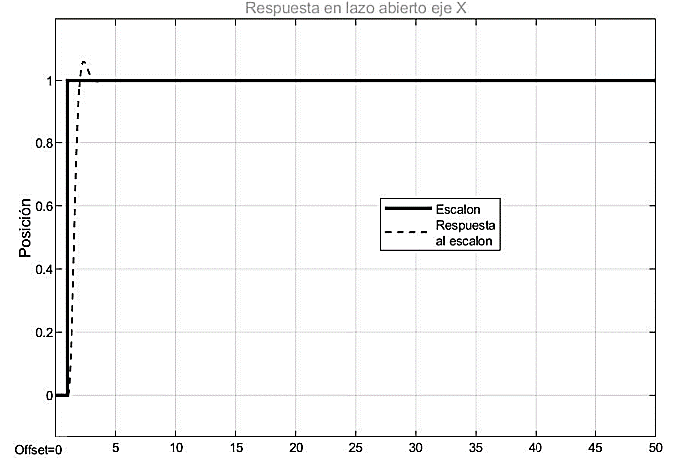
Fig. 7. Respuesta al escalón del sistema con el controlador implementado en el eje X.
Fuente: elaboración propia.
Eje Y:
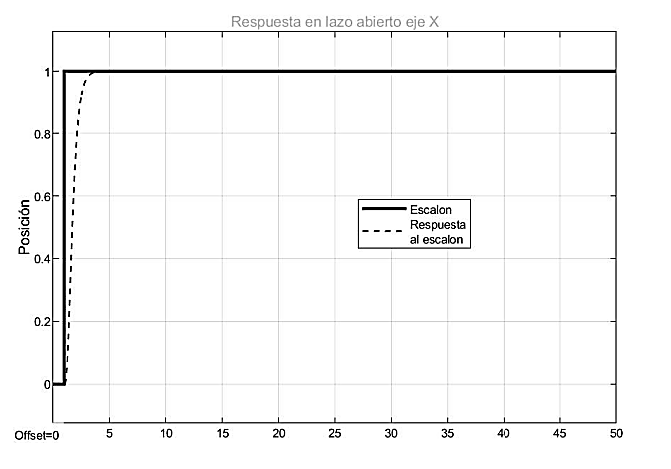
Fig. 8. Respuesta al escalón del sistema con el controlador implementado en el eje Y.
Fuente: elaboración propia.
De esta forma se completa el diseño del controlador LQR PI Vectorial.
4. RESULTADOS
Para comprobar el funcionamiento del controlador se aplicaron diferentes perturbaciones al sistema, para esto se utilizó la misma simulación que se presentó en la figura 6 pero se agregaron las perturbaciones a la salida como se muestra en la figura 9.
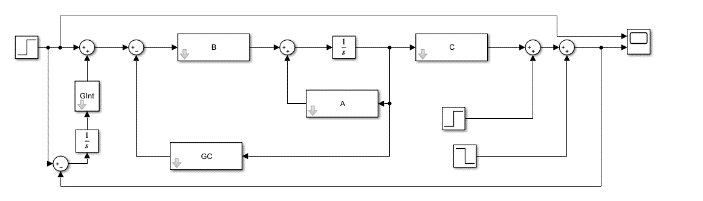
Fig. 9. Diagrama de bloques de los sistemas con el controlador LQR PI Vectorial implementado.
Fuente: elaboración propia.
De esta forma se obtuvo una respuesta ante un impulso con perturbaciones de la siguiente forma.
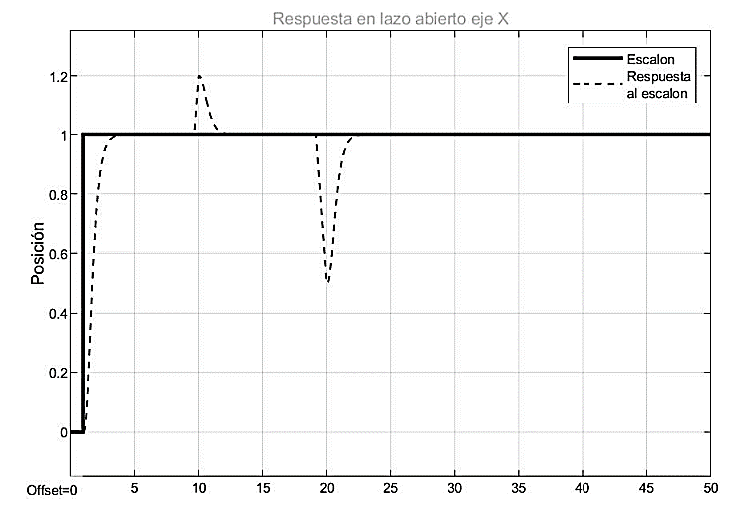
Fig. 10. Respuesta al escalón con perturbaciones del sistema con el controlador implementado en el eje Y.
Fuente: elaboración propia.
Y para el otro eje tendremos una respuesta de la siguiente forma.
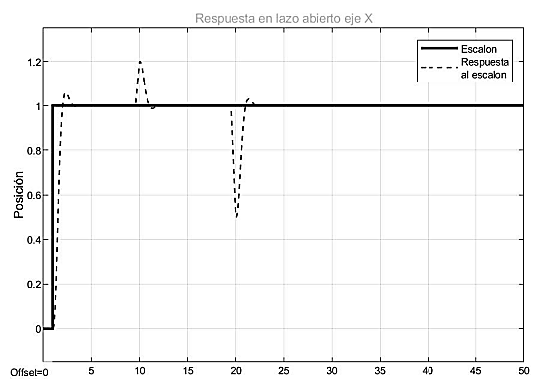
Fig. 11. Respuesta al escalón con perturbaciones del sistema con el controlador implementado en el eje X.
Fuente: elaboración propia.
Como se puede observar en las figuras 10 y 11 el sistema responde bien ante perturbaciones aplicadas ya sea positiva o negativamente, lo cual se traduce en que se puede perturbar efectivamente hacia cualquier dirección en ambos ejes, esto causa que el sistema sea más robusto e incluso llegue a corregir los posibles errores cometidos a la hora de modelar el sistema. Además, suprime casi todas las oscilaciones presentadas, a diferencia que con otros tipos de controladores. A continuación, se presentan las constantes de un controlador PD convencional que se implementó en un principio en el modelo físico, este controlador tiene como constantes:
\[ K_p = 20, \quad K_d = 1.1 \]
De esta forma se pueden comparar las dos respuestas al impulso y verificar la rapidez, eficiencia y precisión de los dos tipos de controladores, en la figura 12 se muestra el diagrama de bloques utilizado en Simulink para la comparación de ambos controladores.
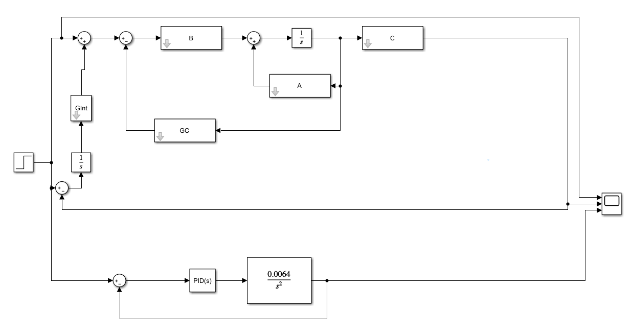
Fig. 12. Diagramas de bloques para la comparación de las respuestas de los controladores.
Fuente: elaboración propia.
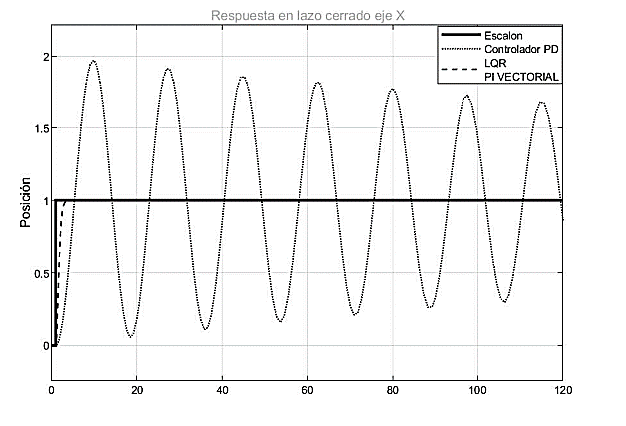
Fig. 13. Respuesta al escalón del sistema con los dos controladores.
Fuente: elaboración propia.
Como se aprecia en la figura 13 la línea con puntos delgados es la respuesta al controlador PD, como se observa, sí se comienza a llevar la bola a la referencia del sistema, sin embargo, se presentan grandes oscilaciones lo cual presentaría en el sistema una alta inestabilidad. Estas oscilaciones también harían que se necesiten acciones de control más grandes y por lo consiguiente mayor esfuerzo en los actuadores, lo que finalmente se traduce como problemas físicos en un futuro. A diferencia de la línea punteada gruesa la cual muestra cómo se llega al valor de referencia con mayor rapidez lo cual presentará una mayor eficiencia y permitirá una mayor durabilidad para los acoples mecánicos del sistema.
5. CONCLUSIONES
Una planta de control “Ball and plate” permite modelar y observar desde un punto de vista académico los problemas generados por las no linealidades que se pueden presentar en procesos reales, además de ser uno de los tipos de sistemas más complicados de controlar debido a su alta inestabilidad inducida por sus grandes oscilaciones, las cuales se presentan en sus dos subsistemas, que debido a su mutua relación se vuelve más complejo el control buscando el error en estado estable igual a 0.
Los controladores utilizados comúnmente son muy poco eficaces ante este tipo de plantas, ya que no son muy precisos y su baja eficacia puede resultar en daños permanentes en el sistema físico. Este inconveniente se puede sortear mediante el uso de un controlador LQR PI Vectorial el cual minimiza las oscilaciones presentes en el sistema y produce una acción de control más precisa que se traduce en mayor tiempo de vida del equipo.
De esta forma se plantea el uso de este tipo de controladores al tener como objetivo de control sistemas de segundo orden con oscilaciones sostenidas.
REFERENCIAS
[1] S. Awtar, C. Bernard, N. Boklund, A. Master, D. Ueda, and K. Craig, “Mechatronic design of a ball-on-plate balancing system,” Mechatronics, vol. 12, no. 2, pp. 217–228, Mar. 2002, doi:
https://doi.org/10.1016/S0957-4158(01)00062-9.
[2] A. H. Frank and M. Tjernström, “Construction and theoretical study of a ball balancing platform Limitations when stabilizing dynamic systems through implementation of automatic control theory,” 2019.
[3] J. Ma, H. Tao, and J. Huang, “Observer integrated backstepping control for a ball and plate system,” Int. J. Dyn. Control, vol. 9, no. 1, pp. 141–148, Mar. 2021, doi:
https://doi.org/10.1007/s40435-020-00629-8.
[4] K. Ogata, Ingenieria de Control Moderno, vol. 53. 1960.
[5] H. M. Díaz, Contabilidad general: enfoque práctico con aplicaciones informáticas. Pearson Education, 2013.
[6] R. C. Dobson, “Sistemas de Segundo Orden,” Univ. Magallanes, pp. 1–13, 2006, Accessed: Oct. 12, 2023. [Online]. Available:
http://ona.fi.umag.cl/~rcdhttp://ona.fi.umag.cl/~rcd.
[7] N. Covic and A. Salihbegovic, “The State-Space Representation of MIMO LTI Systems using the Future Inputs Elimination Approach,” 2023. [Online]. Available:
https://www.researchgate.net/publication/372216658.
[8] D. Rowell, “State-space representation of lti systems,” URL http//web. mit. edu/2.14/www/Handouts/StateSpace. pdf, no. October, pp. 1–18, 2002, Accessed: Oct. 12, 2023. [Online]. Available:
http://www.web.mit.edu/2.14/www/Handouts/StateSpace.pdf%5Cnhttp://files/1757/StateSpace.pdf.
[9] Y. Zhu and Z. Sun, “Minimum realization for controllability/observability of switched linear systems,” Nonlinear Anal. Hybrid Syst., vol. 51, p. 101426, Feb. 2023, doi:
https://doi.org/10.1016/j.nahs.2023.101426.
[10] W. P. M. H. Heemels, S. J. L. Van Eijndhoven, and A. A. Stoorvogel, “Linear quadratic regulator problem with positive controls,” Int. J. Control, vol. 70, no. 4, pp. 551–578, Jan. 1998, doi:
https://doi.org/10.1080/002071798222208.
[11] P. O. M. Scokaert and J. B. Rawlings, “Constrained linear quadratic regulation,” IEEE Trans. Automat. Contr., vol. 43, no. 8, pp. 1163–1169, 1998, doi:
https://doi.org/10.1109/9.704994.
[12] Mangin S, “DEVELOPMENT OF A PROTOTYPE BALL-AND-PLATE BALANCING PLATFORM,” 2022.
[13] Quanser, “2 DOF Ball Balancer Student Workbook,” p. 26, 2013.
[14] D. A. Ratkowsky and G. R. Dolby, “Taylor Series Linearization and Scoring for Parameters in Nonlinear Regression,” Appl. Stat., vol. 24, no. 1, p. 109, Mar. 1975, doi:
https://doi.org/10.2307/2346709.
[15] A.-L. Jaime, “CONSTRUCCION DE HOVER CON DISE NO CONTROLADOR PI VECTORIAL,” 2014, pp. 1–5, [Online]. Available:
https://www.researchgate.net/publication/299385742.















