Simulación numérica de la propagación de ondas en diversos medios usando diferencias finitas
Numeric simulation of wave propagation in some media using finite-difference approach
Resumen: La propagación de las ondas mecánicas es un fenómeno natural o artificial y se transmite en un medio; su propagación se modela utilizando ecuaciones diferenciales en derivadas parciales, las cuales deben resolverse numéricamente. Las derivadas respecto al tiempo y al espacio se resuelven utilizando una aproximación de segundo orden a través de operadores en diferencias finitas centrados. Debido a que el modelado se realiza en profundidad, los valores de los ejes espaciales se consideran positivos cuando esta aumenta. Considerando además velocidades y esfuerzos dentro de una malla escalonada, la cual tiene en cuenta la deformación generada en el medio debido a los esfuerzos y el impacto de la onda en dicho medio. Este efecto de deformación se analizará matemáticamente teniendo en cuenta los coeficientes de Lamé, dado que el medio por donde se propaga la onda es isótropo. También se analizará reflexión y transmisión de la onda para mirar su comportamiento natural. Puesto que el hecho de que el modelado de la onda es computacional, se hace un tratamiento a las condiciones de estabilidad y dispersión numérica para no obtener resultados erróneos y ser capaces de visualizar la onda con un comportamiento más realista. Los métodos de absorción de borde fueron analizados para evitar la visualización de falsas reflexiones no existentes en el medio elástico.
Palabras clave: Diferencias Finitas, medio elástico, tensión, deformación, modelamiento de fenómenos sísmicos.
Abstract: The propagation of mechanical waves is a natural or artificial phenomenon and is transmitted in a medium; its propagation is modeled using partial differential equations, which must be solved numerically. The derivatives with respect to time and space are solved using a second-order approximation through centered finite difference operators. Because the modeling is carried out in depth, the values of the spatial axes are considered positive when depth increases. Also considering velocities and efforts within a stepped mesh, which takes into account the deformation generated in the medium due to the efforts and the impact of the wave in said medium. This deformation effect will be analyzed mathematically taking into account the Lamé coefficients, given that the medium through which the wave propagates is isotropic. Reflection and transmission of the wave will also be analyzed to look at its natural behavior. Since the wave modeling is computational, a treatment is made to the conditions of stability and numerical dispersion to avoid obtaining erroneous results and to be able to visualize the wave with a more realistic behavior. Edge absorption methods were analyzed to avoid the visualization of false reflections not existing in the elastic medium.
Keywords: Finite differences, elastic medium, deformation, seismical modeling.
1. INTRODUCCIÓN
El método de diferencias finitas (DF) se usa tradicionalmente para resolver la ecuación de las ondas acústicas y elásticas, estas ecuaciones describen el movimiento de la onda mediante el uso de derivadas parciales tanto del componente espacial como del temporal. Los métodos permiten la simulación de la propagación de onda en medios heterogéneos de alta complejidad y medios geológicamente elásticos. Los operadores en DF más utilizados son las diferencias centradas de segundo orden. Este método muestra que satisface la condición de estabilidad y la dispersión numérica.
Este documento se organiza de la siguiente manera: la formulación matemática se muestra en la sección 2, y la implementación computacional en la sección 3. La sección 4 muestra la experimentación y la 5 los resultados de las implementaciones. Finalmente, las conclusiones se presentan en la sección 6.
2. FORMULACIÓN MATEMÁTICA
Con el fin de modelar el fenómeno de propagación de ondas sísmicas, es necesario describir primero las fuerzas y tensiones que ocurren en el subsuelo cuando se aplica un pulso de energía que origina una deformación. La Fuente de excitación o pulso de energía en un medio elástico no genera una deformación instantánea en las partículas que lo constituyen, si no que tal deformación requiere una cantidad de tiempo para propagarse en diferentes direcciones desde su punto de origen y recorriendo diversas longitudes del medio perturbado. Este fenómeno es bien conocido por experiencias físicas y eventos que se observan diariamente en nuestro entorno como lo son las olas en superficie del agua, ondas en la cuerda del registro de terremotos o explosiones, vibración de una membrana, entre otros. Estos son algunos de los ejemplos que permiten entender la propagación de movimientos de ondulación mecánica.
Los elementos que conforman el medio experimentan una deformación que permite la transmisión de la perturbación (en este caso en energía que se transmite de una partícula a la otra) desde un punto a otro, de esta forma la onda avanza a través del medio, tal como puede observarse en la figura 1.
Fig. 1. Deformación de las partículas durante la transmisión de una onda transversal (Cerjan, 1985
)
En este proceso la perturbación tiene que superar la resistencia que opone el medio a ser deformado, así como la resistencia al movimiento debido a la inercia. Esta transmisión de energía se lleva a cabo por la transmisión de movimiento desde una partícula a la otra y no por la transmisión del medio como un todo.
Su expresión en ecuaciones diferenciales en derivada parcial y aplicando leyes constitutivas del entorno isotrópico son:
\[ \tau_{xx} = (\lambda + 2\mu) \frac{\partial u}{\partial x} + \lambda \frac{\partial w}{\partial z} \hspace{1cm} (1)\]
\[ \tau_{zz} = (\lambda + 2\mu) \frac{\partial w}{\partial z} + \lambda \frac{\partial u}{\partial x} \hspace{1cm} (2)\]
\[ \tau_{zx} = \mu \left( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right) \hspace{1cm} (3)\]
Donde τ
xx y τ
zz son los componentes en el plano x y z de los tensores de esfuerzos, las fuerzas de tracción en los planos x y z respectivamente. Y τ
zx corresponde a la fuerza de tracción en el plano zx, donde u y w son los componentes del desplazamiento en los ejes x y z, respectivamente. Las variables u y w son las velocidades de las partículas y los parámetros de Lamé son ρ y μ, siendo μ la rigidez y ρ es la densidad del medio.
La formulación paso a paso de un esquema de malla dado por Madariaga (1976)
donde lo expresa en términos de velocidad de partículas y tensiones, el movimiento de la ecuación de onda elástica usando un modelo de expansión circular en el medio elástico, y Virieux (1984)
el cual adaptó el esquema general para modelar las ondas en un sistema cartesiano bidimensional. Estos esquemas facilitan el uso de la simulación computacional. Para este sistema cartesiano las ecuaciones que describen movimiento para la velocidad de las ondas compresionales (P) y transversales (S) son:
\[ \rho \frac{\partial u_t}{\partial t} = \frac{\partial \tau_{xx}}{\partial x} + \frac{\partial \tau_{xz}}{\partial z} \hspace{1cm} (4)\]
\[ \rho \frac{\partial w_t}{\partial t} = \frac{\partial \tau_{zx}}{\partial x} + \frac{\partial \tau_{zz}}{\partial z} \hspace{1cm} (5)\]
Las velocidades de compresión y la tasa de cizalla son respectivamente:
\[ \alpha = \mu \sqrt{\frac{\lambda + 2\mu}{\rho}} \hspace{1cm} (6)\]
\[ \beta = \sqrt{\frac{\mu}{\rho}} \hspace{1cm} (7)\]
Tomando la primera derivada con respecto al tiempo de las ecuaciones de las leyes constitutivas del medio, y sustituyendo el término de velocidad de las partículas por desplazamiento, proporciona un sistema de primer orden de las ecuaciones de velocidades y esfuerzos que pueden resolverse numéricamente, Levander (1988)
.
2.1. Propagación en medio acústico
En la exploración sísmica se adquieren datos mediante la aplicación de pulsos de energía, y su consiguiente registro en dispositivos geófonos, con el fin de determinar la estratigrafía del subsuelo. El modelado sísmico es una técnica computacional que permite reconstruir mediante simulaciones los fenómenos de reflexión y refracción de energía en el subsuelo. De esta manera se puede simular la adquisición de datos, y confrontar los registros reales con registros sintéticos. Para poder llevar a cabo el proceso de modelado, es preciso especificar las expresiones para la deformación en un medio elástico, que luego permita deducir las fórmulas de propagación de onda en dicho medio.
2.2. Propagación en medio elástico
El modelo matemático que describe la propagación de vibraciones en una cuerda o las ondas acústicas en el aire se denomina la ecuación de onda, la cual se clasifica como una ecuación diferencial en derivada parcial de tipo hiperbólico. La velocidad de la onda se determina por las propiedades físicas del medio en el que se propaga, donde c2 = F/ρ, F es la fuerza de tensión aplicada y ρ la densidad del material. La ecuación típica de onda se muestra en la expresión 8.
\[ \frac{{\partial^2 u}}{{\partial t^2}} = c^2 \frac{{\partial^2 u}}{{\partial x^2}} \hspace{1cm} (8)\]
Dado que el medio en que se propagan las ondas en el subsuelo no se considera acústico, deben tomarse las definiciones de tensores de deformación y de esfuerzo para modelar la propagación de la energía en un medio elástico. En las ecuaciones anteriores, se ha considerado que estos tensores y los campos asociados están en equilibrio. Sin embargo, cuando hay una perturbación y se propagan ondas, las partículas del subsuelo se aceleran, toman velocidad y se desplazan. De manera que la expresión 8 se puede reformular en la expresión 9.
\[ \rho \frac{{\partial^2 \overline{u}}}{{\partial t^2}} = \theta_j \tau_{ij} + f_i \hspace{1cm} (9)\]
Conociendo la ecuación de movimiento para un medio elástico con propiedades isótropas se procede a deducir la ecuación de onda a resolver para un medio en el plano
xz. Partiendo de la expresión 8 y siendo
u = (ux, uy, uz) = (u, v, w), para el plano
xz se tiene que
u = (u, 0, w) y la expresión en coordenadas cartesianas se escribe de la siguiente manera:
\[ \rho \frac{{\partial^2 u}}{{\partial t^2}} = \partial_j \tau_{xj} = \frac{{\partial \tau_{xx}}}{{\partial x}} + \frac{{\partial \tau_{xz}}}{{\partial z}} \]
\[ \rho \frac{{\partial^2 w}}{{\partial t^2}} = \partial_j \tau_{zj} = \frac{{\partial \tau_{zx}}}{{\partial x}} + \frac{{\partial \tau_{zz}}}{{\partial z}} \hspace{1cm} (10)\]
Aplicando la definición de τ
ij en la expresión 9 se obtienen las definiciones para los tensores:
\[ \tau_{xx} = (\lambda + 2\mu) \frac{\partial u}{\partial x} + \lambda \frac{\partial w}{\partial z} \]
\[ \tau_{xz} = \mu \left( \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} \right) \]
\[ \tau_{zz} = (\lambda + 2\mu) \frac{\partial w}{\partial z} + \lambda \frac{\partial u}{\partial z} \hspace{1cm} (11)\]
Una vez planteadas estas expresiones, pueden resolverse utilizando métodos computacionales.
3. IMPLEMENTACIÓN COMPUTACIONAL
Una primera aproximación se llevó a cabo usando entorno computacional basado en Matlab para Windows, López (2017)
usando un esquema de diferencias finitas en medio acústico. Con este ejemplo en mente, se plantea un esquema de implementación computacional buscando propiedades de estabilidad numérica y tratando de eliminar las falsas reflexiones.
3.1 Discretización usando diferencias finitas
Las coordenadas x y z se discretizan haciendo: x = (m±1)*h, z = (n±1)*h y t = (l ±1) * t´, donde h es el intervalo de la cuadrícula de diferencias finitas y t´ es la muestra del tempo en diferencias finitas.
\[ D_i^+ u_i (m,n,l-\frac{1}{2}) = \frac{1}{\rho(m,n)} \left[ D_x^- \tau_{xx} \left(m+\frac{1}{2}, n, l\right) + D_z^- \tau_{xz} \left(m, n+\frac{1}{2}, l\right) \right] \]
\[ D_i^+ \tau_{zz} \left( m+\frac{1}{2}, n, l \right) = \mu \left( m, n+\frac{1}{2}, l \right) \left[ D_z^- u_t \left( m, n, l+\frac{1}{2} \right) + D_x^- w_t \left( m+\frac{1}{2}, n+\frac{1}{2}, l+\frac{1}{2} \right) \right] \hspace{1cm} (12)\]
\[ D_i^+ \tau_{xz} \left( m+\frac{1}{2}, n, l \right) = \mu \left( m, n+\frac{1}{2}, l \right) \left[ D_z^+ u_t \left( m, n, l+\frac{1}{2} \right) + D_z^- w_t \left( m+\frac{1}{2}, n+\frac{1}{2}, l+\frac{1}{2} \right) \right] \]
Donde \( D_i^+ \) es el operador diferencia con respecto al tiempo en la iteración posterior y \( D_i^+ \tau_{zz} \) y \( D_i^+ \tau_{xz} \) son los operadores diferenciales con respecto al espacio en la iteración posterior y anterior.
3.2. Propiedades de estabilidad y dispersión
Para un medio estándar homogéneo el análisis espectral se ejecuta en el dominio de la frecuencia y da la siguiente condición de estabilidad, Levander (1988)
:
\[ c_p \frac{\Delta t}{\Delta x} \sqrt{\frac{1}{\Delta x^2} + \frac{1}{\Delta z^2}} < 1 \hspace{1cm} (13)\]
Donde Cp es la velocidad de la onda P. Esta condición de estabilidad es independiente de la velocidad de la onda S. Para el caso especial de una malla homogénea la condición de estabilidad es:
\[ c_p \frac{\Delta t}{\Delta x} < \frac{1}{\sqrt{2}} \hspace{1cm} (14)\]
3.3. Atenuación de falsas reflexiones
Al momento de usar el método de diferencias finitas para modelar la propagación, se genera un problema de falsas reflexiones en los bordes de la matriz utilizada para la simulación. En un fenómeno real como cuando ocurre un terremoto, la fuerte explosión de energía que se genera en tales momentos, causa una onda que continúa su trayectoria a través del subsuelo hasta que pierde toda su energía. Puesto que la simulación es computacional, tiene lugar en un área en la cual la onda que transmite su energía es limitada por el tamaño de la malla (matriz) que se esté utilizando. Se generan fronteras artificiales las cuales generan reflexiones inexistentes que se traducen en ruidos o datos falsos. Para reducir esas falsas reflexiones, el esquema descrito por Cerjan (1985)
se ha implementado, con bordes de 20 nodos de ancho para cada frontera de la malla. En estos bordes se reduce ligeramente con cada paso de tiempo el valor propagado (paso de la onda en los bordes seleccionados). La reducción en cada borde seleccionado se estrecha gradualmente desde cero en la frontera interior. Los nodos entre 1 y 20 de cada borde se multiplican por este factor:
\[ G = e^{-[0.015 \cdot (20 - i)]^2} \hspace{1cm} (15)\]
Donde i toma valores entre 1 y 20 que corresponden al nodo en el cual está pasando el frente de onda. G toma los valores de 1 para i = 20 y un valor de 0.92 para i = 1. Este esquema puede utilizarse en el modelado con métodos como elementos finitos y el método de Fourier, Pasalic C. y McGarry
. En la figura 2 se puede apreciar un esquema de absorción de bordes en la frontera superior de la malla.
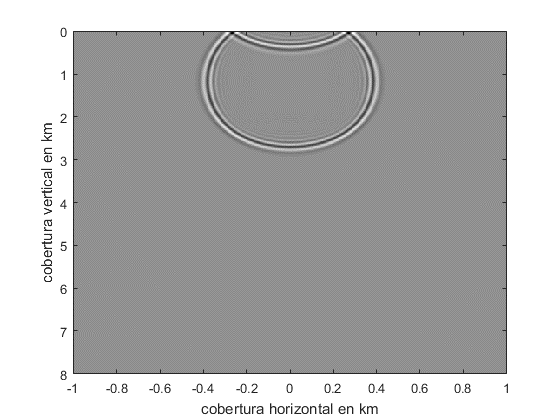
(a)
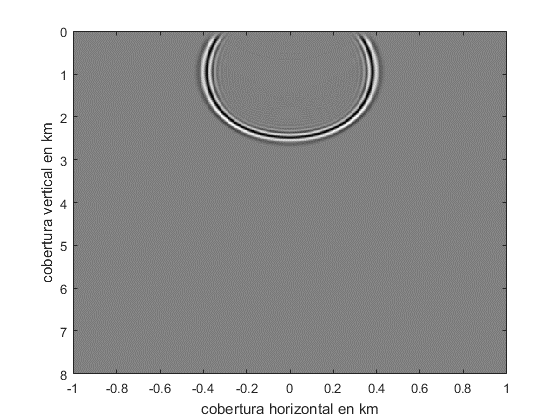
(b)
Fig. 2. Comparación del esquema de reducción de la reflexión de la onda en los bordes. La parte a muestra el modelado de la onda sin la atenuación y la parte b es la atenuación de la absorción de los bordes izquierdo e inferior con coeficiente G.
4. EXPERIMENTOS NUMÉRICOS
El medio está en equilibro en el tiempo t = 0, es decir, las componentes de velocidades y de esfuerzos son cero. Propagar los esfuerzos y las velocidades equivale a propagar sus componentes en todo el tiempo, Virieux (1986)
. Las derivadas de primer grado se discretizan usando diferencias finitas centradas con una aproximación de octavo orden de acuerdo a los pesos dados por el código propuesto por Fornberg (1988)
y se asignan a cada nodo. La principal diferencia con los esquemas habituales es que los componentes de los coeficientes de Lamé y de densidad del medio no se conocen en el mismo nodo, como se muestra en la figura 4. Para calcular los símbolos cuadrados y circulares, los parámetros de Lamé y la densidad son necesarios en el tiempo tΔt y para calcular los símbolos triangulares los coeficientes de Lamé son necesarios en el tiempo (t+½)Δt.
Las dimensiones de la malla se suponen de 500x500, cubriendo una anchura de 2km, y una profundidad de 8 km respectivamente, a una frecuencia fundamental de 20 hz con dos capas planas paralelas, lo que origina tres regiones donde la velocidad es diferente. Los valores de Δx y Δz serían de 4m y 16m respectivamente.
En cuanto a las capas planas, la primera va desde la superficie hasta los 2km de profundidad, y se asume una velocidad de 2000 m/s; la segunda va de los 2km a los 4km de profundidad asumiendo una velocidad de 3000 m/s, la última se extiende desde los 4km hasta los 8km con una velocidad de 4000 m/s.
La implementación computacional se llevó a cabo en una máquina Intel i5, con 3.3 GHz de velocidad de procesador y se utilizó el entorno de programación matlab.
En las diversas experimentaciones, se simularon dos reflectores ubicados a 1000 y 2000 m ubicados por debajo de la fuente, que está a 100 m de la superficie.
5. DISCUSIÓN DE RESULTADOS
Una vez efectuadas simulaciones con 800 iteraciones, se pueden apreciar resultados demostrando la factibilidad de la solución computacional a problemas de este tipo. Las figuras 3 y 4 muestran los efectos de las capas en la reflexión y refracción de la onda que se propaga.
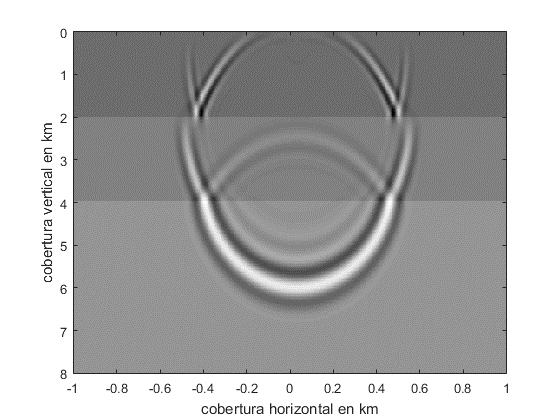
Fig. 3. Propagación de la onda en dos capas de densidades diferentes en t=0.45s.

Fig. 4. Propagación de la onda en dos capas de densidades diferentes en t=0.85s.
También se puede apreciar el perfil de velocidades considerando dos reflectores durante un tiempo de simulación de 0.85s. Aquí se considera que la fuente está cercana a 0 en el eje horizontal.
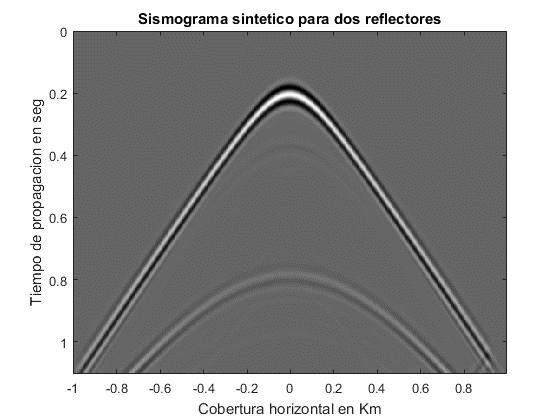
Fig. 5. Perfil de velocidades considerando dos reflectores.
Como se puede apreciar en la figura 5, se aprecian varias velocidades, debido al paso de la onda por las diversas capas, y la reflexión de parte de ella que genera un movimiento en sentido contrario.
La figura 6 de la amplitud de la onda a una profundidad de 1800m es la siguiente:
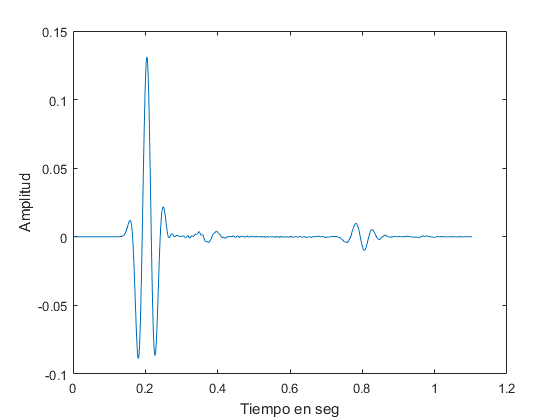
Fig. 6. Amplitud de la onda durante la simulación.
Como puede apreciarse, se aprecian dos reflexiones de la onda a los 0.2s y 0.8s debido al paso por capas diferentes, considerando que en el tiempo 0 se produjo la excitación inicial.
6. CONCLUSIONES
El trabajo realizado demuestra que es factible simular la propagación de una onda en un esquema de geología compleja, mediante una representación explícita usando diferencias finitas. Este esquema de implementación permite ejecutar una simulación aproximada para la realidad de la transferencia de la onda en el medio elástico. Además, este modelado permite simular la adquisición de datos sísmicos con varios reflectores, así como con mayor cantidad de capas y otras disposiciones, tales como sinclinales.
El componente vertical del sismograma permite una mayor visualización de las reflexiones de la onda cuando se transmiten en un medio elástico. Debido al comportamiento de la onda y las diversas reflexiones que presenta, ocasionan que esta simulación sea algo complicada de entender o visualizar claramente lo cual hace que sea necesario utilizar esquemas que reduzcan las reflexiones de los bordes ya que esto complicaría aún más el análisis del sismograma.
El esquema de atenuación de reflejos en los bordes reduce en alto grado las falsas reflexiones en los bordes de la malla aún a pesar de que no elimina completamente esas reflexiones y debido a la simulación de los geófonos en la parte superior de la malla no es de gran ayuda en el borde.
REFERENCIAS
[1] Cerjan C. (1985). “A nonreflecting boundary condition for discrete acoustic and elastic wave equations”. Geophysics, vol 50, P 705-708.
[2] Madariaga, R. (1976). “Dynamics of an expanding circular fault, Bull”. Seismic Society Am., 66, 639-666.
[3] Virieux, J. (1984). “SH-Wave propagation in heterogeneous media: velocity-stress finite-difference method”. Geophysics, vol 49, P 1933-1957.
[4] Levander, R. (1988). “Fourth-order finite-difference P-SV seismograms”. Geophysics, vol 53, P 1425-1436.
[5] López, J. (2017). “Diseño de un algoritmo empleando métodos numéricos para solucionar la ecuación de onda en un medio elástico bidimensional”. Universidad de Pamplona. Ingeniería de Sistemas, 2017.
[6] Pasalic C. y McGarry R. (2010). “Convolutional perfectly matched layer for isotropic and anisotropic acoustic wave equations”. 2010 Seg Annual Meeting.
[7] Virieux, J. (1986). “P-SV wave propagation in heterogeneous media: velocity-stress finite-difference method”. Geophysics, vol 51 Issue 4, P 889-901.
[8] Fornberg, B. (1988). “Generation of Finite Difference Formulas on Arbitrarily Spaced Grids”. Mathematics of Computation, 51, 699-706.


 1,
PhD. José Orlando Maldonado Buautista
1,
PhD. José Orlando Maldonado Buautista 1,
MSc. Luis Armando Portilla Granados
1,
MSc. Luis Armando Portilla Granados 1
1







