Arreglos fotovoltaicos con estructura cruzada con configuración irregular: un modelo
Resumen: Los sistemas fotovoltaicos (FV) son ampliamente usados en entornos urbanos para producir electricidad. Esas instalaciones FV se diseñan para aprovechar espacios no usados como techos, donde se tienen otros dispositivos instalados (antenas, chimeneas, etc.), por lo que el espacio disponible no es regular. Por lo tanto, se debe diseñar un modelo matemático que tenga en cuenta esas irregularidades en la instalación FV. Este artículo introduce un nuevo modelo para ese tipo de instalaciones PV irregulares, el cual usa una formulación implícita de la característica corriente-voltaje de los módulos, permitiendo de esta forma evitar el uso de cálculos complejos como la función Lambert-W, lo que reduce el tiempo de cálculo. El modelo se basa en un sistema de ecuaciones formulado a partir de las relaciones circuitales de la estructura cruzada, la cual es una candidata ideal para instalaciones FV irregulares. Finalmente, el modelo se valida usando una instalación FV realista, la cual está basada en módulos FV comerciales.
Palabras clave: Arreglo fotovoltaico irregular, ejemplo de aplicación, formulación implícita, reducción del tiempo de cálculo, software Simulink/Matlab.
Abstract: Photovoltaic (PV) systems are extensively used in urban environments to produce electricity. Those PV installations are designed to take profit from unused spaces such as rooftops, where many other devices are installed (antenna, chimney, etc.), thus the available space is not regular. Therefore, a mathematical model must be designed to take into account those irregularities in the PV configuration. This paper introduces a new model for those irregular PV installations, which uses an implicit formulation of the current-voltage characteristic of the modules, thus avoiding costly mathematical computations like the lambert-W function to reduce the calculation time. The model is based on an equation system formulated from the circuital relations of the total cross tied structure, which is a suitable candidate for irregular PV installations. Finally, the model is validated using a realistic PV installation based on commercial PV modules.
Keywords: Application example, calculation time reduction, implicit formulation, irregular photovoltaic array, Simulink/Matlab software.
1. INTRODUCCIÓN
La energía fotovoltaica (FV) es una de las fuentes renovables que está dirigiendo la transición energética mundial
. Muchos generadores fotovoltaicos se están instalando en techos de casas, edificios y otras estructuras con formas o superficies irregulares
. Los arreglos irregulares son comunes en aquellas superficies donde existen restricciones de espacios de instalación en contraste con la cantidad de energía eléctrica requerida; por ejemplo, en techos de casas y edificios, es necesario aprovechar el espacio debido a la forma irregular de sus tejados o a la presencia de elementos como chimeneas, antenas, etc. Ver Fig. 1. También cuando los arreglos en Total Cross Tied (TCT) son reconfigurados, la configuración óptima podría ser un array irregular para evitar la activación de los diodos de bypass (BD). Para diseñar y operar arreglos irregulares, los módulos FV se representan con modelos matemáticos que utilizan la función Lambert-W aumentando el tiempo de cálculo del arreglo
y, por lo tanto, reduciendo la extracción de potencia durante el proceso de reconfiguración del arreglo FV. Consecuentemente, se requieren modelos matemáticos de arreglos irregulares para calcular las curvas I-V y P-V reduciendo el tiempo de procesamiento.
El objetivo de este artículo es proponer un modelo matemático para calcular las curvas corriente-voltaje y potencia-voltaje de arreglos irregulares, los cuales son comunes en espacios de instalación irregulares y luego de las reconfiguraciones de arreglos TCT. El modelo utiliza una formulación implícita de la relación corriente-voltaje de cada módulo, evitando el uso de la función Lambert-W, la cual aumenta el tiempo de cálculo. Con este modelo rápido y preciso es posible estimar la potencia máxima en el proceso de diseño de arreglos fotovoltaicos y también en su reconfiguración.
El resto del artículo está organizado de la siguiente forma: en la Sección 2, se presenta el modelado del módulo fotovoltaico; luego, el modelo matemático de los arreglos TCT irregulares se describe en la Sección 3, incluyendo un ejemplo para explicar el concepto propuesto. La Sección 4 presenta la validación del modelo propuesto mediante simulaciones. Esta sección incluye el desarrollo matemático del problema y simulaciones en el software PSIM. La financiación y las conclusiones están en las Secciones 5 y 6, respectivamente.
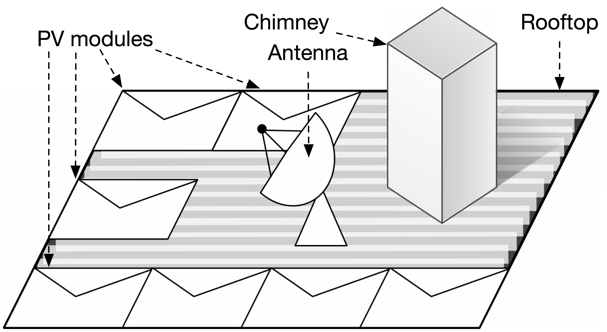
Fig. 1. Techo con espacios irregulares
2. MODULO FOTOVOLTAICO
Dado que los arreglos FV están formados por módulos FV, el primer paso del modelo es describir, mediante expresiones matemáticas, el comportamiento de un módulo FV. La representación más adoptada para módulos FV, basada en un circuito equivalente, se presenta en la Fig. 2. Este modelo de circuito se denomina Single Diode Model (SDM), ya que la unión PN de la fuente FV se modela con el diodo, D. La resistencia paralela (R
h) modela la corriente de fuga y la resistencia en serie (R
s) modela las pérdidas óhmicas. Adicionalmente, el modelo de la Fig. 2 incluye el BD.
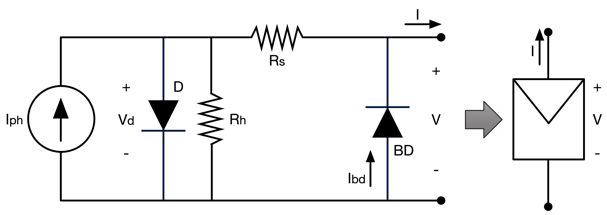
Fig. 2. Modelo circuital de un módulo FV incluyendo el diodo de bypass
La formulación matemática de esta representación circuital fue analizada en
, la cual provee una expresión implícita que no requiere la función Lambert-W
, evitando el gran esfuerzo computacional requerido por esa operación especializada. En resumen, la expresión que relaciona la corriente y el voltaje del módulo es dada en (1), donde I y V son la corriente y el voltaje del módulo, respectivamente.
\[ f(V,I) = -I + I_{ph} - I_{D} - I_{Rh} + I_{BD} \hspace{1cm} (1)\]
\[ I_D = I_S \left[e^{\frac{V_d}{N_s \cdot \eta \cdot V_t}} - 1\right] \hspace{1cm} (2)\]
\[ I_{Rh} = \frac{V_d}{R_h} \hspace{1cm} (3)\]
\[ V_d = V + (I - I_{BD}) \cdot R_s \hspace{1cm} (4)\]
\[ I_{BD} = I_{S,BD} \left[e^{\frac{V}{\eta_{BD} \cdot V_{t,BD}}} - 1\right] \hspace{1cm} (5)\]
I
ph es la corriente fotovoltaica, que es casi proporcional a la irradiancia solar que llega al módulo fotovoltaico. IS, η y V
t son la corriente de saturación inversa, el factor de idealidad y el voltaje térmico del módulo fotovoltaico; N
s corresponde al número de celdas conectadas en serie que forman el módulo. De manera similar, I
S,BD, η
BD y V
t,BD son la corriente de saturación inversa, el factor de idealidad y el voltaje térmico del diodo de bypass. Esos parámetros se pueden extraer tanto de la hoja de datos como de las mediciones experimentales utilizando el método reportado en
.
3. ARREGLO TCT IRREGULAR
Los arreglos TCT irregulares están formados por filas con diferente número de módulos. Por ejemplo, la matriz TCT irregular instalada en el techo del ejemplo de la Fig. 1 se describe eléctricamente en la Fig. 3, que está formada por tres filas: la primera tiene dos módulos conectados en paralelo (M1 y M4), la segunda tiene un único módulo (M2), y la tercera tiene cuatro módulos conectados en paralelo (M3, M5, M6 y M7). El índice del módulo se asigna numerando los módulos de arriba a abajo en cada columna y luego cambiando a la siguiente columna para comenzar desde arriba nuevamente. Teniendo en cuenta que todos los módulos de una misma fila tienen el mismo voltaje, los voltajes de las filas se asignan numerando los voltajes de las filas de arriba a abajo. Además, el tamaño del arreglo se describe en términos del número de filas (N) y el número máximo de columnas del arreglo (M); por lo tanto, el arreglo de la Fig. 3 tiene N = 3 y M = 4.
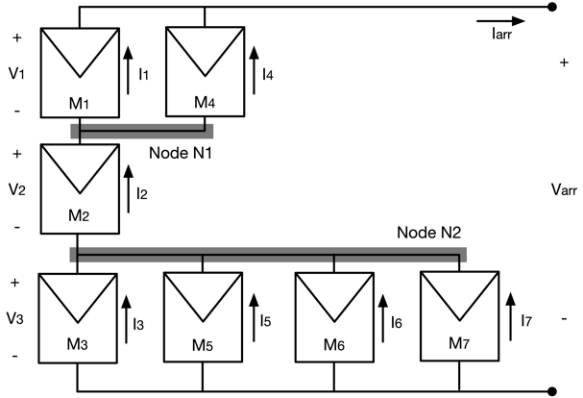
Fig. 3. Arreglo TCT irregular (N = 3 y M = 4)
Los parámetros de los módulos que forman el arreglo se describen dentro de las matrices con la nomenclatura descrita anteriormente, donde los parámetros de los módulos faltantes se reportan con valor 0. Por ejemplo, la corriente fotovoltaica I
ph de todos los módulos en el arreglo de la Fig. 3 se reportan en la siguiente matriz:
\[
M_{I_{ph}} = \begin{bmatrix}
5.5 & 4.5 & 0 & 0 \\
2.5 & 0 & 0 & 0 \\
5.5 & 2.5 & 4.5 & 4.5
\end{bmatrix}
\hspace{1cm} (6)\]
En la matriz anterior, la corriente fotovoltaica del módulo M1 es de 5,5 A, mientras que la corriente I
ph del módulo M6 es de 4,5 A. De esta forma, la matriz M
Iph proporciona todas las corrientes fotovoltaicas del arreglo. Se utiliza el mismo procedimiento para describir I
S, η, V
t, N
s, R
s, R
h, I
S,BD, η
BD y V
t,BD para todos los módulos del arreglo, esto utilizando las matrices correspondientes M
Is, M
η, M
Vt, M
Ns, M
Rs, M
Rh, M
Is,BD, M
η,BD, M
Vt,BD.
Para analizar el arreglo FV, es necesario calcular los voltajes y corrientes de los módulos: N voltajes (Vr) y NM corrientes del módulo (Im), donde NM es el número de elementos distintos de cero de la matriz M
Iph. Así, las variables desconocidas quedan dadas de la siguiente manera:
\[
V_r = \begin{bmatrix} V_1 & V_2 & \dots & V_N \end{bmatrix}^T
\hspace{1cm} (7)\]
\[
I_m = \begin{bmatrix} I_1 & I_2 & \dots & I_{N_m} \end{bmatrix}^T
\hspace{1cm} (8)\]
Luego, el sistema de ecuaciones no lineales que describe el arreglo FV se construye con N
m ecuaciones de corriente de cada módulo FV, de igual forma que en (1), la suma de los voltajes de todas las filas igual al voltaje del arreglo, y N-1 ecuaciones de las corrientes de Kirchhoff de cada nodo del arreglo FV, es decir, las conexiones entre filas; la Fig. 4 muestra los dos nodos (N1 y N2) para el arreglo TCT. Finalmente, la Fig. 4 muestra la estructura general del sistema de ecuaciones que se resuelve para encontrar las corrientes y voltajes de los módulos, es decir, las ecuaciones (7) y (8).
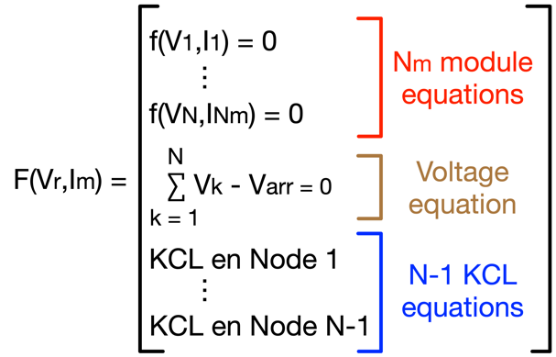
Fig. 4. Estructura del sistema de ecuaciones
El sistema de ecuaciones anterior puede ser resuelto usando un método numérico o algoritmo de optimización; por ejemplo, usando la función fsolve() de Matlab.
4. VALIDACIÓN CIRCUITAL
La validación del modelo propuesto es desarrollada usando el arreglo del ejemplo mostrado en la Fig. 4 (N = 3 and M = 4). Este arreglo FV tiene 10 variables desconocidas (3 voltajes y 7 corrientes) tal y como se reporta en las ecuaciones (9) y (10).
\[
V_r = \begin{bmatrix} V_1 & V_2 & V_3 \end{bmatrix}^T
\hspace{1cm} (9)\]
\[
I_m = \begin{bmatrix} I_1 & I_2 & I_3 & I_4 & I_5 & I_6 & I_7 \end{bmatrix}^T
\hspace{1cm} (10)\]
Luego, aplicando el procedimiento de modelado reportado en la Sección 3, el sistema de ecuaciones resultantes necesario para encontrar las variables desconocidas es dado en la Fig. 5.
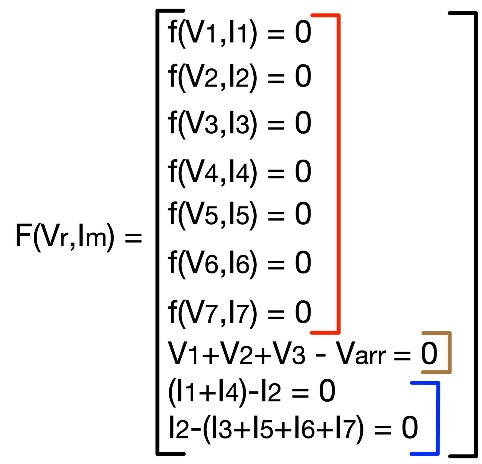
Fig. 5. Sistema de ecuaciones del ejemplo del arreglo
TCT (N = 3 and M = 4)
El módulo FV considerado para las simulaciones fu el ERDM 85, el cual está formado por 36 celdas conectadas en serie (N
s = 36) y un diodo de bypass. Los parámetros del SDM fueron obtenidos usando un procedimiento propuesto en
obteniendo los siguientes valores para una temperatura de 25 °C y una irradianza de 1 kW/m2: I
ph = 5.133 A, η = 1.061, I
s = 1.184 A, R
s = 186.4 m𝛺, and R
h = 261.09 𝛺. Además, los parámetros del diodo de bypass usados para las simulaciones fueron: ηBD = 0.269 y I
S,BD = 1.00 𝜇A. La temperatura asumida para las celdas y los diodos de bypass fue de 25 °C; donde, V
t = V
t,BD = 25.7 mV. Aunque los mismos parámetros fueron usados para todos los módulos (except I
ph), Es importante resaltar que el modelo es el mismo, aunque cada módulo y diodo de bypass del arreglo tenga diferentes parámetros.
Las simulaciones consideran tres escenarios representados en las matrices M
Iph1, M
Iph2 y M
Iph3 mostradas abajo, que representan el parámetro I
ph de los módulos del arreglo para condiciones uniformes (M
Iph1) y dos condiciones no uniformes diferentes (M
Iph2 and M
Iph3).
\[
M_{I_{ph1}} = 5.133 \begin{bmatrix}
1.0 & 1.0 & 0 & 0 \\
1.0 & 0 & 0 & 0 \\
1.0 & 1.0 & 1.0 & 1.0
\end{bmatrix}
\]
\[
M_{I_{ph2}} = 5.133 \begin{bmatrix}
0.5 & 0.5 & 0 & 0 \\
1.0 & 0 & 0 & 0 \\
0.25 & 0.25 & 0.25 & 0.25
\end{bmatrix}
\]
\[
M_{I_{ph3}} = 5.133 \begin{bmatrix}
0.25 & 0.25 & 0 & 0 \\
1.0 & 0 & 0 & 0 \\
0.5 & 0.5 & 0.25 & 0.25
\end{bmatrix}
\]
El circuito equivalente del arreglo fue implementado en Simulink/Matlab para calcular el error del modelo propuesto versus la implementación circuital. Los resultados de simulación están en la Fig. 6, donde las curvas obtenidas con el modelo propuesto son presentadas en azul y los desde Simulink son presentados en rojo con líneas continuas, a trazos y punteadas para M
Iph1, M
Iph2, y M
Iph3, respectivamente.
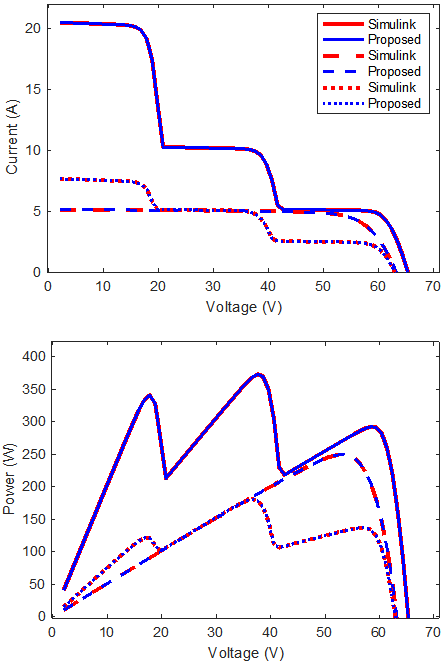
Fig. 6. Resultados de simulación para un arreglo TCT irregular para 3 condiciones de operación. MIph1: líneas continuas, MIph2: líneas a trazos, MIph3: líneas punteadas.
Para todos los casos, el modelo propuesto reproduce los resultados de la implementación circuital con la suma normalizada del cuadrado de los errores (NSSE) de 4.2e-12%, 9.3e-12%, and 24.1e-12% para M
Iph1, M
Iph2, and M
Iph3, respectivamente.
Las curvas I-V y P-V para MIph1 indican que una configuración TCT irregular puede proveer múltiples puntos de potencia máxima (MPPs) aún si todos los módulos están operando bajo la misma irradianza (i.e. condiciones uniformes). Además, las curvas I-V y P-V para M
Iph2 y M
Iph3 muestran que arreglos TCT irregulares pueden ser usados para compensar condiciones de irradianza no uniformes. Como puede ser observado, M
Iph2 y M
Iph3 tienen los mismos módulos organizados en dos formas diferentes; pero con el orden provisto por M
Iph2, la suma de I
ph en cada fila es la misma (1.0 A); donde, la curva del arreglo P-V tiene solamente un MPP. Sin embargo, con el orden provisto por M
Iph3 la curva P-V tiene tres MPPs y todos ellos son menores que el MPP obtenido con M
Iph2. Esto indica que el modelo propuesto puede ser usado para implementar algoritmos de reconfiguración basados en modelo u otras aplicaciones que requieran el cálculo de las curvas I-V and P-V de arreglos TCT irregulares.
5. CONCLUSIONES
En este artículo se propuso un modelo matemático que utiliza una formulación implícita de la relación corriente-voltaje de cada módulo FV para representar arreglos FV irregulares. A partir del modelo circuital se derivó un sistema de ecuaciones para representar cada módulo; Posteriormente, se utilizó un arreglo TCT irregular para ilustrar el procedimiento de solución. Finalmente, el modelo propuesto fue validado mediante la formulación del sistema de ecuaciones de un arreglo irregular de 3x4 y su simulación utilizando el software Simulink/Matlab. La comparación de los resultados de simulación mostró que el modelo propuesto es adecuado para implementar algoritmos de reconfiguración basados en modelos u otras aplicaciones que requieren el cálculo de las curvas I-V y P-V de arreglos TCT irregulares, que se usan comúnmente en techos de casas, edificios y otras estructuras.
AGRADECIMIENTOS
Esta investigación fue financiada por Minciencias, la Universidad Nacional de Colombia, la Universidad del Valle, y la institución universitaria ITM b ajo el proyecto de investigación “Dimensionamiento, planeación y control de sistemas eléctricos basados en fuentes renovables no convencionales, sistemas de almacenamiento y pilas de combustible para incrementar el acceso y la seguridad energética de poblaciones colombianas” (Minciencias code 70386), el cual pertenece al programa de investigación “Estrategias para el desarrollo de sistemas energéticos sostenibles, confiables, eficientes y accesibles para el futuro de Colombia” (Minciencias code 1150-852-70378, Hermes code 46771).
REFERENCIAS
[1] P. Frankl, “Energy System Debate: What Lies Ahead for the Future [In My View]”, IEEE Power and Energy Magazine, Vol. 17, No. 2, 2019, pp. 100-98.
[2] Key, “Finding a bright spot”, IEEE Power and Energy Magazine, Vol. 7, No. 3, 2009, pp. 34-44.
[3] G. Petrone, G. Spagnuolo, and M, Vitelli, “Analytical model of mismatched photovoltaic fields by means of Lambert W-function”, Solar Energy Materials and Solar Cells, Vol. 91, No. 18, 2007, pp. 1652–1657.
[4] J. D. Bastidas-Rodriguez, C. A. Ramos-Paja, and A. J. Saavedra-Montes, “Implicit mathematical model of photovoltaic arrays with improved calculation speed based on inflection points of the current–voltage curves”, Energies, Vol. 16, No. 13, 2023, p. 4875.
[5] R.M. Corless, G.H. Gonnet, D.E.G. Hare, D.J. Jeffrey, D.E. Knuth, “On the Lambert W function”, Advances in Computational Mathematics, Vol. 5, No. 1, 1996, pp 329–359.
[6] J. Accarino, G. Petrone, C. A. Ramos-Paja and G. Spagnuolo, “Symbolic algebra for the calculation of the series and parallel resistances in PV module model”, 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 2013, pp. 62-66.


 1,
PhD. Carlos Andrés Ramos-Paja
1,
PhD. Carlos Andrés Ramos-Paja 2,
PhD. Andrés Julián Saavedra-Montes
2,
PhD. Andrés Julián Saavedra-Montes 2
2






