Modelización y simulación de un compensador estático síncrono para sistemas de distribución de energía eléctrica
Modeling and simulation of a static synchronous compensator for power distribution systems
Resumen: En este artículo se aborda la modelización y simulación de un DSTATCOM (Compensador Estático Síncrono de Distribución) en conexión shunt para compensar un sistema eléctrico de potencia. La simulación en el software seleccionado determinará el desempeño, la estabilidad, la corrección del factor de potencia y la regulación de tensión en sistemas de distribución trifásicos. El comportamiento del DSTATCOM será probado en simulación ante una condición que afecte la calidad de la energía del sistema.
Palabras clave: VSC, PWM, D-STATCOM, potencia reactiva, potencia activa, PCC.
Abstract: This paper deals with the modeling and simulation of a DSTATCOM (Distribution Synchronous Static Synchronous Compensator) in shunt connection to compensate an electrical power system. The simulation in the selected software will determine the performance, stability, power factor correction and voltage regulation in three-phase distribution systems. The behavior of the DSTATCOM will be tested in simulation under a condition that affects the power quality of the system.
Keywords: VSC, PWM, D-STATCOM, reactive power, active power, PCC.
1. INTRODUCCIÓN
En la industria, en el comercio y residencias son muchos los equipos eléctricos y electrónicos que contienen inductancias y capacitancias, como son los motores eléctricos, transformadores, inductancias en fuentes electrónicas, entre otras
. Lo anterior genera que los sistemas de potencia deban proporcionar no sólo energía útil como lo es el caso de la energía activa, sino que deben cada vez más aportar más energía reactiva, la cual disminuye la capacidad de transporte de energía útil. Por otro lado, es importante destacar que en la conexión y desconexión de los dispositivos electrónicos y cargas no lineales se producen “perturbaciones” en los sistemas eléctricos que también desmejoran la forma de la onda sinusoidal tanto en tensión como en corriente
.
La aplicación de sistemas de compensación con electrónica de potencia se realiza desde los años 1970
con la introducción del tiristor creado por General Electric y la aplicación del IGBT por Mitsubishi Electric en la misma década (ver anexos para la nomenclatura utilizada). Posteriormente se desarrollaron varios dispositivos en electrónica de potencia como es el caso del Compensador Estático Síncrono, STATCOM
.
El D-STATCOM es un dispositivo FACTS, siendo este una aplicación del STATCOM en SEP de redes de distribución, cuyo propósito es compensar la potencia reactiva manteniendo la tensión de la red eléctrica. Este dispositivo puede inyectar corrientes en atraso o en adelanto independiente de la tensión del sistema eléctrico
.
Su conexión se realiza principalmente en derivación o shunt cuando se conecta al punto común de conexión, PCC, tal y como se muestra en la figura 1.

Fig. 1. Diagrama de bloques del D-STATCOM.
2. PRINCIPIO DE OPERACIÓN Y MODELIZACIÓN DEL D-STATCOM
2.1. Principio de operación
El D-STATCOM puede suprimir las variaciones de tensión en el bus de tensión o también llamado PCC (ver figura 1), compensando la potencia reactiva del sistema de distribución de energía eléctrica conforme a su requerimiento. Esto se logra aplicando una tensión mayor (V
D-STACOM) a la tensión del bus o barraje (V
BUS), donde se inyecta la potencia reactiva a la red eléctrica aumentando el valor de tensión en el PCC y en caso contrario, (V
D-STACOM) se reduce con respecto a V
BUS para que compensador consuma potencia reactiva, reduciendo de esta forma el valor de tensión en el PCC
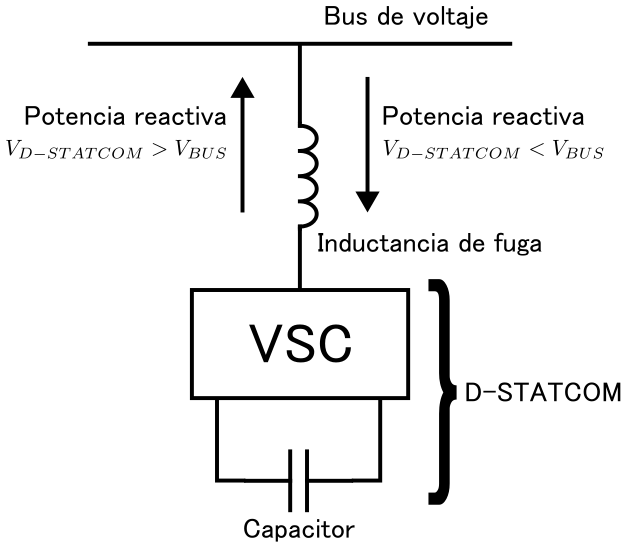
Fig. 2. Principio de operación del D-STATCOM.
2.2. Modelización del D-STATCOM
En la figura 3 se muestra con mayor detalle la conexión del D-STATCOM en el punto PCC
. Aunque más adelante se utilizara en la simulación un filtro LCL, en la figura solo se muestra una inductancia L junto con su resistencia interna R. La resistencia r_oncorresponde a la resistencia interna de cada transistor IGBT.
El D-STATCOM se controla utilizando un sistema de referencia dq, para lo cual se deben medir las corrientes por fase que entregue el VSC y así calcular las corrientes en cuadratura i
d e i
q. El PLL estima el ángulo ρ y las tensiones por fase del VSC se operan para calcular las tensiones en cuadratura V
sd y V
sq. Estas medidas alimentan los controladores utilizando un sistema de referencia dq que se utiliza para entregar la modulación m
d y m
q, necesaria para transformarse a un sistema abc y que se comparada con la portadora del circuito PWM.
Fig. 3. Sistema completo D-STATCOM, carga y fuente trifásica.
Aplicando leyes de Kirchhoff de corriente y tensión se obtienen las expresiones en el PCC.
\[ V_{sa} = L_{g} \frac{{d\mathrm{i}_{ga}}}{{dt}} + V_{ga} + V_{\text{null}} \hspace{1cm} (1)\]
\[ V_{sb} = L_{g} \frac{{d\mathrm{i}_{gb}}}{{dt}} + V_{gb} + V_{\text{null}} \hspace{1cm} (2)\]
\[ V_{sc} = L_{g} \frac{{d\mathrm{i}_{gc}}}{{dt}} + V_{gc} + V_{\text{null}} \hspace{1cm} (3)\]
\[ i_{ga} = i_{a} - i_{La} \hspace{1cm} (4)\]
\[ i_{gb} = i_{b} - i_{Lb} \hspace{1cm} (5)\]
\[ i_{gc} = i_{c} - i_{Lc} \hspace{1cm} (6)\]
La tensión V
null corresponde a la tensión del centro de la conexión del generador de referencia a 0V.
Utilizando la transformación vector espacial es decir al transformar del sistema de referencia trifásico abc al sistema de referencia en Park o en cuadratura dq0 según lo explicado en el anexo Representación en vector espacial se cumple:
\[ \vec{V_s} = L_g \frac{d\vec{i_g}}{dt} + \vec{V_g} \hspace{1cm} (7)\]
\[ \vec{i_g} = i - \vec{i_L} \hspace{1cm} (8)\]
\[ \vec{V_g} = \hat{V_g} e^{j(\omega_0 t + \theta_0)} \hspace{1cm} (9)\]
El D-STATCOM se controla en el sistema de referencia dq0 y estará sincronizado a un ángulo de rotación ρ.
Sustituyendo en (7) la siguiente representación vectorial:
\[ \vec{V_s} = V_{sdq} e^{j\rho} \hspace{1cm} (10)\]
\[ \vec{i_g} = i_{gdq} e^{j\rho} \hspace{1cm} (11)\]
\[ \vec{V_g} = \hat{V_g} e^{j(\omega_0 t + \theta_0)} \hspace{1cm} (12)\]
se tiene
\[ V_{sdq} e^{j\rho} = L_g \frac{d}{dt} \left(i_{gdq} e^{j\rho} \right) + \hat{V_g} e^{j(\omega_0 t + \theta_0)} \hspace{1cm} (13)\]
\[ V_{sa} = L_g \frac{di_{ga}}{dt} + V_{ga} + V_{\text{null}} \hspace{1cm} (14)\]
\[ V_{sdq} e^{j\rho} = L_g \frac{d}{dt} \left( i_{gdq} e^{j\rho} \right) + \hat{V_g} e^{j(\omega_0 t + \theta_0)} \hspace{1cm} (15)\]
\[ L \frac{di_d}{dt} = L \omega_0 i_q - (R + r_{\text{on}}) i_d + V_d - V_{sd} \hspace{1cm} (16)\]
\[ L \frac{di_q}{dt} = L \omega_0 i_d - (R + r_{\text{on}}) i_q + V_d - V_{sq} \hspace{1cm} (17)\]
Siendo la potencia activa y reactiva en el PCC en el sistema de referencia dq como
:
\[ P_s = \frac{3}{2} [V_{sd}(t) i_d(t) + V_{sq}(t) i_q(t)] \hspace{1cm} (18)\]
\[ Q_s = \frac{3}{2} [-V_{sd}(t) i_q(t) + V_{sq}(t) i_d(t)] \hspace{1cm} (19)\]
El D-STATCOM utiliza un control de corriente debido a que el control por tensión no respondería correctamente ante una falla de corto circuito
. Es por ello que el controlador en dq utiliza las variables de control de corriente i
d e i
q por lo tanto el sistema sigue sin error i
dref e i
qref que se calculan con (18) y (19).
\[ i_{d\text{ref}}(t) = \frac{2}{3} V_{\text{sd}} P_{\text{sref}}(t) \hspace{1cm} (20)\]
\[ i_{q\text{ref}}(t) = \frac{2}{3} V_{\text{sd}} Q_{\text{sref}}(t) \hspace{1cm} (21)\]
Con las ecuaciones (20) y (21) se calculan los valores de referencia para una potencia activa, P y potencia reactiva Q deseada, aunque en el caso del D-STATCOM sólo se controla la potencia activa requerida para compensar las pérdidas del dispositivo.
En la sección 5 de simulación se muestran estas referencias utilizando la tensión del enlace de corriente continua V
DC para calcular el valor necesario de potencia activa junto con el valor de tensión V
D necesario para conseguir la potencia reactiva requerida, tal y como se muestra en la figura 3.
3. SIMULACIÓN
El núcleo del D-STATCOM es el VSC donde en lado de DC tiene conectado un capacitor C (Farhad et al., 2015). Este dispositivo se acopla al SEP a través de una inductancia de filtrado. El VSC lo conforma un puente trifásico de IGBTs, cada uno con un diodo en antiparalelo que actúa como rectificador.
La figura 4 se muestran el diagrama de bloques que integra la simulación con el software Simulink de Matlab.
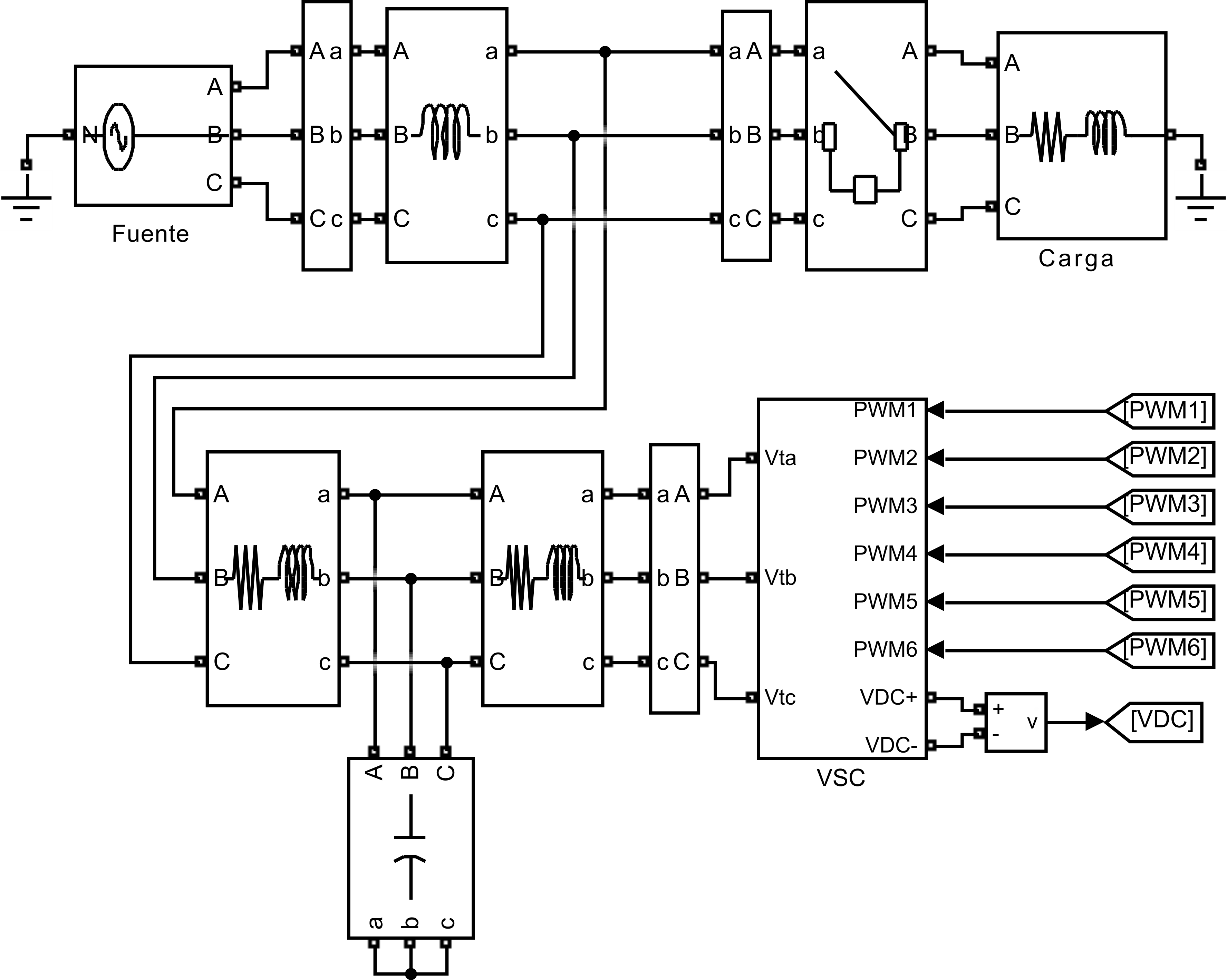
Fig. 4. D-STATCOM conectado a PCC en circuito multifilar en Matlab.
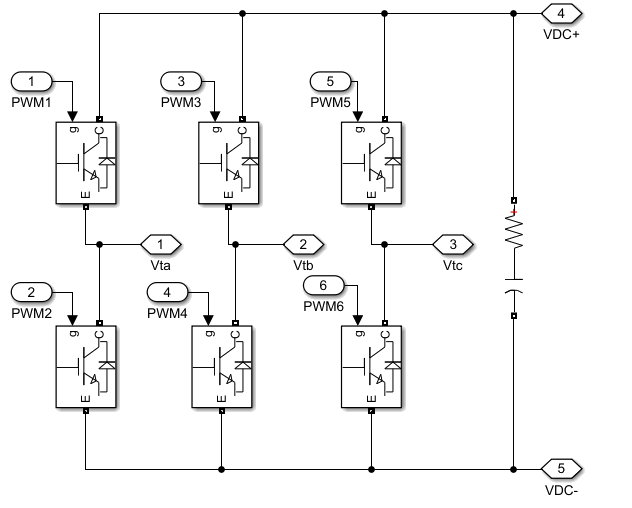
Fig. 5. Puente trifásicos de IGBTs.
EN este módulo se utiliza una modulación PWM para los disparos de cada interruptor IGBT (ver figura 5), comparando la señal moduladora calculada por el circuito de control y que se compara con una señal portadora de más alta frecuencia que la moduladora (ver figura 3).
EN la figura 6 se muestra la lógica utilizada para la generación de las señales PWM. El circuito de control calcula las tensiones en el sistema de referencia dq para luego calcularse en el sistema de referencia abc.
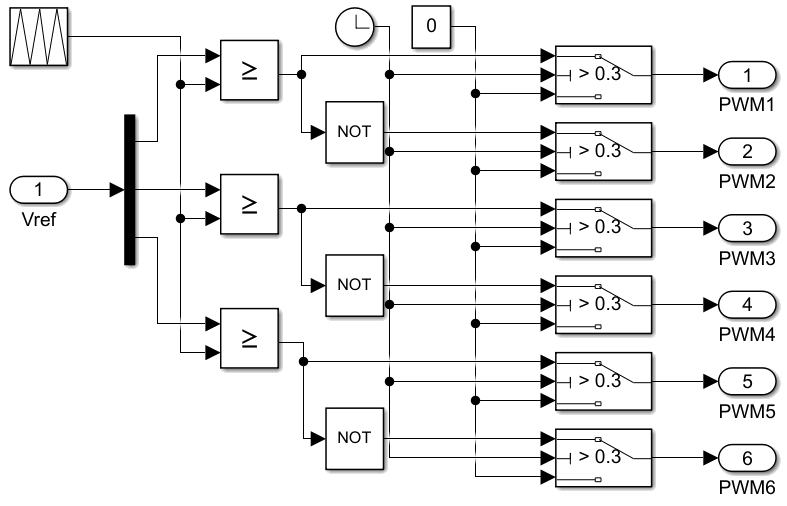
Fig. 6. Subsistema para generación de señal PWM.
La figura 7, propuesta por (Murugesan & Muthu, 2011), calcula la señal de corriente i_(d )e i_q partiendo de la referencia V_DC y V_d, respectivamente, y esta se compara con el valor medido en el bus DC y la tensión V_d que se mide en el PCC.
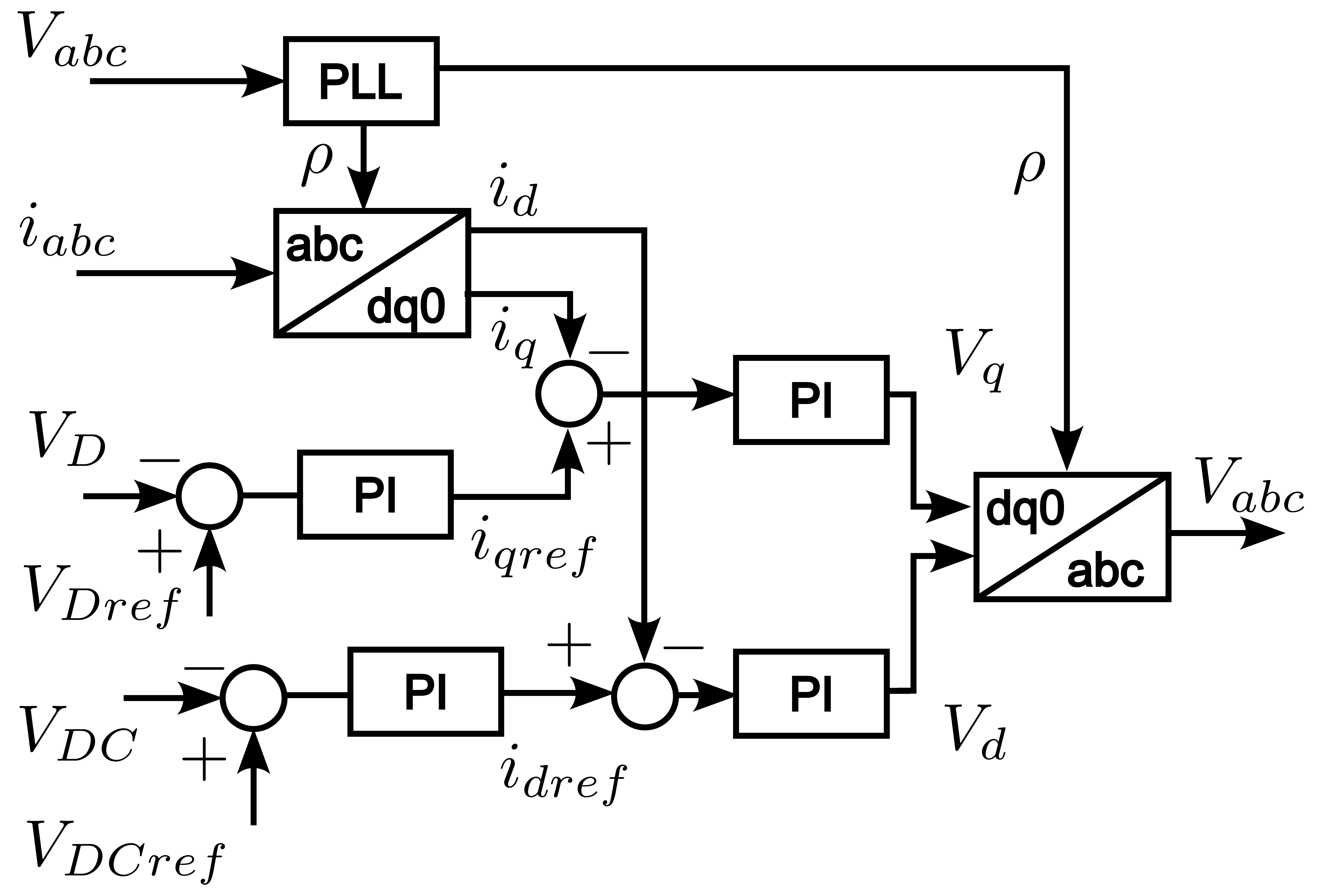
Fig. 7. D-STATCOM conectado a PCC en circuito multifilar.
Tabla 1: descripción
| Elemento o dispositivo |
Valor |
Observaciones |
| VDC |
2500 V |
Tensión del bus DC |
| C |
1000 uF |
Capacitancia del VSC |
| Carga |
80 kW |
Potencia activa carga |
| 40 kVAR |
Potencia reactiva carga |
| Generador |
2.7 mH |
Ls Inductancia del generador |
| 480 V |
Tensión línea a línea |
| Filtro LCL |
623 uH |
Li inductancia del lado del VSC |
| 374 mH |
Lg inductancia del lado del generador |
| 46 uF |
Cf capacitancia del filtro LCL |
Fuente: Valores de los elementos del circuito
Ejecutando la simulación se observa en la figura 8 que a partir de 0 segundos hasta 0.2 segundos la tensión en los terminales del VSC es el provisto por los diodos conectados a los IGBTs que operan como rectificador trifásico. En el tiempo 0.2 se conecta la carga al circuito de potencia y nótese una caída en la tensión de los terminales del VSC. Posteriormente en 0.3 segundos se habilitan las señales de control en los IGBTs donde se observa una señal difusa en la gráfica, que corresponde con la modulación PWM trifásica.
Fig. 8. Tensión en los terminales del D-STATCOM.
En la figura 9 se detalla un acercamiento entre el tiempo 0.297 segundos hasta el tiempo 0.309 aproximadamente y se muestran la modulación PWM que al promediarse sigue una señal aproximadamente sinusoidal.
Fig. 9. Zoom en el tiempo de la tensión en los terminales del D-STATCOM.
En esta simulación se ha configurado la señal moduladora tiene una frecuencia de 60 Hz y la señal de la portadora de 10kHz.
El circuito de la figura 5 muestra la fuente trifásica y en la parte derecha la carga. Conectado al PCC a través de un filtro LCL donde se muestran las modulaciones que han sido calculadas de forma individual y no se ha utilizado el bloque STATCOM que con el que cuenta la toolbox de Matlab.
El filtro LCL logra el acoplamiento y también el filtrado en corriente y tensión con el propósito de mejorar las medidas que van al controlador.
Fig. 10. Respuesta del D-STATCOM al cambio de tensión.
En la figura 10 se muestra la respuesta a la variación de tensión en el PCC. La grafica se detalla desde 0 segundos y alcanzándolos 0.15 segundos la medida se estabiliza. La tensión mostrada es V_d que corresponde a la amplitud de la tensión pico de la tensión de fase, es decir:
\[ V_{LL} = 480 \, \text{V} \]
\[ V_{\text{fase}} = \frac{480}{\sqrt{3}} = 277.13 \, \text{Vrms} \]
\[ V_{\text{fase pico}} = 391.91 \, \text{V} \]
En la figura 11 el PCC con el generador en vacío alcanza una tensión de 450 V pico. En 0.2s se cierra el interruptor automático del circuito y se logra mostrar el transitorio de la conexión de la carga, logrando descender la tensión en el PCC a 350 V pico. En 0.3s donde se habilita el puente de IGBTs del VSC y se nota una recuperación de la tensión en el PCC. Obsérvese que del dispositivo alcanza una tensión pico de 392 V aproximadamente en 0.9s.
Fig. 11. Tensión y corriente en la carga.
La figura 12 y 13 muestran la tensión y corriente en la fuente trifásica y en el VSC respectivamente.
Fig. 12. Tensión y corriente del alternador.
Fig. 13. Tensión y corriente del alternador.
4. CONCLUSIONES
Aplicando leyes físicas como las leyes de Kirchhoff se logró plantear las ecuaciones dinámicas que describen el comportamiento del sistema de AC con carga y acoplado a un VSC.
Utilizando Simulink de Matlab se realizó la simulación del SEP y el sistema de control del VSC para la compensación de la tensión en el PCC.
El D-STATCOM presenta una respuesta rápida ante perturbaciones siendo efectivo para mantener los niveles de tensión en rangos aceptables.
El D-STATCOM mejora la estabilidad del SEP, previniendo caídas de tensión y oscilaciones debido a su rápida respuesta de compensación.
Dado que el D-STATCOM compensa potencia reactiva, mejora el factor de potencia del SEP y contribuyendo a una mejor calidad de la energía para los usuarios finales.
El D-STATCOM al ser un convertidor de DC a AC igual que los inversores de sistemas de energías renovables, haría que estos últimos puedan integrarse como compensadores en el SEP, modificándoles el sistema de control del VSC.
El D-STATCOM al mejorar el factor de potencia con su aporte de potencia reactiva en el SEP, se amplía la capacidad de transporte de energía útil en la red de distribución haciendo más eficiente al SEP.
Es importante que los sistemas de medición de corrientes y tensión en el PCC, VSC y cargas sean los mejores, ya que unas medidas incorrectas pueden hacer que el D-STATCOM aporte valores incorrectos de potencia reactiva y con ultima causar inestabilidad en el SEP.
Es importante revisar y ajustar los esquemas de protección del D-STATCOM al SEP ya que un mal ajuste puede perjudicar la coordinación de protecciones del SEP.
Los valores de ganancias de los controladores PI en lazo i_d e i_q dependen de los valores de la resistencia interna de la inductancia de fuga, la resistencia de encendido del IGBT, r_on y las inductancias de fuga que en este articulo fueron L_i y L_g.
Al simular el D-STATCOM se encontró que debe haber un procedimiento al ir habilitando cada uno los diferentes componentes que lo conforman. Es preferible iniciar con los capacitores cargados antes que los IGBTs sean desbloqueados para su funcionamiento.
REFERENCIAS
[1] P. Khetarpal and M. M. Tripathi, “A critical and comprehensive review on power quality disturbance detection and classification,” Sustainable Computing: Informatics and Systems, vol. 28, p. 100417, Dec. 2020, doi:
10.1016/j.suscom.2020.100417.
[2] O. K. Shinde and V. R. S. V. B. Pulavarthi, “STATCOM converters and control: A review,” in 2017 International Conference on Data Management, Analytics and Innovation, ICDMAI 2017, Institute of Electrical and Electronics Engineers Inc., Oct. 2017, pp. 145–151. doi:
10.1109/ICDMAI.2017.8073500.
[3] T. Jing and A. S. Maklakov, “A Review of Voltage Source Converters for Energy Applications,” in Proceedings - 2018 International Ural Conference on Green Energy, UralCon 2018, Institute of Electrical and Electronics Engineers Inc., Nov. 2018, pp. 275–281. doi:
10.1109/URALCON.2018.8544364.
[4] N. G. Hingoranl, L. Gyugyi, and M. E. El-Hawary, Understanding FACTS: Concepts and technology of flexible ac transmission systems. 1999. doi:
10.1109/9780470546802.
[5] S. S. Parimal Borse, Dr. A. G. Thosar, “Modeling and Simulation of STATCOM,” International Journal of Engineering Research and Technology (IJERT), vol. 3, no. 12, pp. 200–203, 2014, Accessed: Jul. 22, 2023. [Online]. Available:
www.ijert.org
[6] A. Yazdani and R. Iravani, Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications. IEEE Press/John Wiley, 2010. doi:
10.1002/9780470551578.
[7] H. Akagi, Y. Kanazawa, and A. Nabae, “Instantaneous Reactive Power Compensators Comprising Switching Devices without Energy Storage Components,” IEEE Trans Ind Appl, vol. IA-20, no. 3, pp. 625–630, 1984, doi:
10.1109/TIA.1984.4504460.
[8] S. Farhad, R. Sumedha, and G. Arindam, Static Compensators (STATCOMs) in Power Systems. 2015.
[9] X.-P. Zhang and Z. Yan, “Energy Quality: A Definition,” IEEE Open Access Journal of Power and Energy, vol. 7, no. September, pp. 430–440, 2020, doi:
10.1109/oajpe.2020.3029767.
ANEXOS
Anexo A: Nomenclatura
FACTS Flexible Alternating Current Transmission System
STATCOM Static Synchronous Compensator
D-STATCOM Distribution Static Synchronous Compensator
DC Direct current
AC Alternating current
VSC Voltage Source Converter
VA Voltage-Ampere
IGBT Insulated Gate Bipolar Transistor
SEP Sistema eléctrico de potencia
P Active Power
PLL Phase Locked Loop
Q Reactive Power
PWM Pulse Width Modulation
LCL Filtro inductor capacitor inductor
Anexo B: Representación en fasor espacial
El autor
en su obra Voltage-sourced converters in power systems modeling control and applications realiza la transformación del marco abc al marco dq0 utilizando representación en fasor espacial o Space Phasor. La conversión se realiza para sistemas trifásicos utilizando las siguientes ecuaciones:
\[ f_a(t) = \hat{f} \cos(\omega t + \theta_0) \]
\[ f_b(t) = \hat{f} \cos(\omega t + \theta_0 - \frac{2\pi}{3}) \]
\[ f_c(t) = \hat{f} \cos(\omega t + \theta_0 - \frac{4\pi}{3}) \]
Siendo \( \hat{f} \), \( \theta_0 \) y \( \omega \) la amplitud, ángulo inicial de desfase y velocidad angular del fasor.
\( \vec{f}(t) = \frac{2}{3} \left[ e^{j0} f_a(t) + e^{j\frac{2\pi}{3}} f_b(t) + e^{j\frac{4\pi}{3}} f_c(t) \right] \)















