Revista Colombiana de
Tecnologías de Avanzada
Tecnologías de Avanzada
Recibido: 14 de marzo de 2022
Aceptado: 26 de septiembre de 2022
Aceptado: 26 de septiembre de 2022
USE OF DAILY PRECIPITATION CONCENTRATION INDEX AS A TOOL FOR ESTIMATING THE MOST HYDROLOGICAL RELEVANT MONTHS IN CHAMBAS BASIN
USO DEL ÍNDICE DE CONCENTRACIÓN DE PRECIPITACIÓN DIARIA COMO HERRAMIENTA PARA ESTIMAR LOS MESES MÁS HIDROLÓGICAMENTE RELEVANTES EN LA CUENCA DE CHAMBAS
 Dr.C. Enrique Almeida Maldonado*,
Dr.C. Enrique Almeida Maldonado*,
 Dr.C. Yoelkis Hernández Víctor*,
Dr.C. Yoelkis Hernández Víctor*,
 Dr.C. Oscar Brown Manrique*,
Dr.C. Oscar Brown Manrique*,
 Dr.C. Juan Antonio Martín Alfonso*,
Dr.C. Juan Antonio Martín Alfonso*,
 Dr.C. Francisco García Reina*.
Dr.C. Francisco García Reina*.
* Universidad de Ciego de Ávila Máximo Gómez Báez (UNICA), Cuba.
E-mail: ealmeida.cu@gmail.com
{yoelkis, obrown, jamartin, pancho}@unica.cu
USO DEL ÍNDICE DE CONCENTRACIÓN DE PRECIPITACIÓN DIARIA COMO HERRAMIENTA PARA ESTIMAR LOS MESES MÁS HIDROLÓGICAMENTE RELEVANTES EN LA CUENCA DE CHAMBAS
 Dr.C. Enrique Almeida Maldonado*,
Dr.C. Enrique Almeida Maldonado*,
 Dr.C. Yoelkis Hernández Víctor*,
Dr.C. Yoelkis Hernández Víctor*,
 Dr.C. Oscar Brown Manrique*,
Dr.C. Oscar Brown Manrique*,
 Dr.C. Juan Antonio Martín Alfonso*,
Dr.C. Juan Antonio Martín Alfonso*,
 Dr.C. Francisco García Reina*.
Dr.C. Francisco García Reina*.
* Universidad de Ciego de Ávila Máximo Gómez Báez (UNICA), Cuba.
E-mail: ealmeida.cu@gmail.com
{yoelkis, obrown, jamartin, pancho}@unica.cu
Cómo citar: Almeida Maldonado, E., Hernández Víctor, Y., Brown Manrique, O., Martín Alfonso, J. A., & García Reina, F.
(2022). USO DEL ÍNDICE DE CONCENTRACIÓN DE PRECIPITACIÓN DIARIA COMO HERRAMIENTA PARA ESTIMAR LOS MESES MÁS HIDROLÓGICAMENTE RELEVANTES EN LA
CUENCA DE CHAMBAS. REVISTA COLOMBIANA DE TECNOLOGIAS DE AVANZADA (RCTA), 2(40), 95-102.
https://doi.org/10.24054/rcta.v2i40.2357
Derechos de autor 2022 Revista Colombiana de Tecnologías de Avanzada (RCTA).
Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.

Abstract: The Chambas basin, located in the province of Ciego de Ávila, Cuba is the main source of supply for the territory
it crosses and has been the object of the development of hydraulic projects. This study examined the monthly distribution of precipitation, to
determine the most relevant periods from a hydrological point of view. For this, traditional statistical measures were used in combination
with the daily precipitation concentration index. The results showed that the months with the lowest precipitation concentration index are
April, May, June, July, August and September, while from October to March they had the highest values, indicating that these months accumulate
more precipitation in fewer days. of rain. October was identified as the month of greatest interest for agricultural activity and engineering
work, due to its high historical rainfall averages. It was concluded that the concentration index, calculated monthly, in combination with
other statistics, is a useful tool and provides relevant information.
Keywords: Concentration index, Monthly rainfall, Daily precipitation, Precipitation indices, Monthly analysis, daily maximum rainfall.
Resumen: La cuenca Chambas, ubicada en la provincia de Ciego de Ávila, Cuba es la principal fuente de suministro para el territorio que atraviesa y ha sido objeto del desarrollo de proyectos hidráulicos. Este estudio examinó la distribución mensual de la precipitación, para determinar los períodos más relevantes desde un punto de vista hidrológico. Para ello, se utilizaron las medidas estadísticas tradicionales en combinación con el índice de concentración diaria de precipitación. Los resultados mostraron que los meses con menor índice de concentración de precipitación son abril, mayo, junio, julio, agosto y septiembre, mientras que de octubre a marzo tuvieron los valores más altos, lo que indica que estos meses acumulan mayor precipitación en menos días de lluvia. Octubre fue identificado como el mes de mayor interés para la actividad agrícola y labores de ingeniería, debido a sus altos promedios históricos de precipitación. Se concluyó que el índice de concentración, calculado mensualmente, en combinación con otras estadísticas, es una herramienta útil y proporciona información relevante.
Palabras clave: Índice de concentración, precipitación mensual, precipitación diaria, índices de precipitación, análisis mensual, máxima precipitación diaria.
In particular, extreme rainfall events on a daily scale are characterized by durations limited to a small number of days; however, they represent a high percentage of monthly, seasonal and annual precipitation
In these investigations, the CI has shown to be a reliable estimator of the degree of aggressiveness or rainfall torrentiality, being also explanatory of processes of slope instability, as well as the risks of flooding and drought. However, in all the works carried out, it has been used to characterize the historical behavior of areas from their total records. That is, in no case has a study of this variable been carried out on a monthly basis, even though it is evident that there are differences, significant for various processes, in the way in which rainfall is distributed during the different stages of the year. In the present work a study of the behavior of the daily concentration coefficient at a monthly level is carried out for the Chambas river basin; with the objective of describing the behavior of the accumulation of rainfall in each month. In this way, a useful and practical tool can be obtained to determine which month (s) of the year represent the greatest interest from a hydrological point of view.
From the hydrological point of view, a system of dams, micro dams and canals has been built along it with the aim of avoiding floods and supplying water for the development of agriculture, livestock, industry and consumption.
In Cuba, two periods are typically recognized according to their rainfall: one dry, which includes the months from November to April, and the other rainy from May to October
As can be seen, the behavior of the basin is similar in general terms to the rest of the country with regard to the distribution of its months in the dry and rainy periods. It is under this criterion that decisions of various kinds are generally made; however, the authors of this work consider that it is also important to take into account the way in which rain is distributed on a daily basis; that is, the daily concentration of precipitation, since it is a measure that characterizes the way how the rain falls in a given period.
In terms of the statistical structure of daily precipitation, the distribution of its quantity frequencies is, in general, adjustable by negative exponential distributions, since, when classifying and tabulating the quantities of daily precipitation by longitude, their absolute frequencies decrease exponentially
In order to evaluate the relative contribution of the rainiest days in a given period, Martín Vide proposed a daily precipitation concentration index (CI)
To extract the data at the monthly level for the basin, the records of the values contributed by the 12 rain gauges were analyzed as a whole. In this way, for each month the exponential curve of the type of equation (4) was calculated.
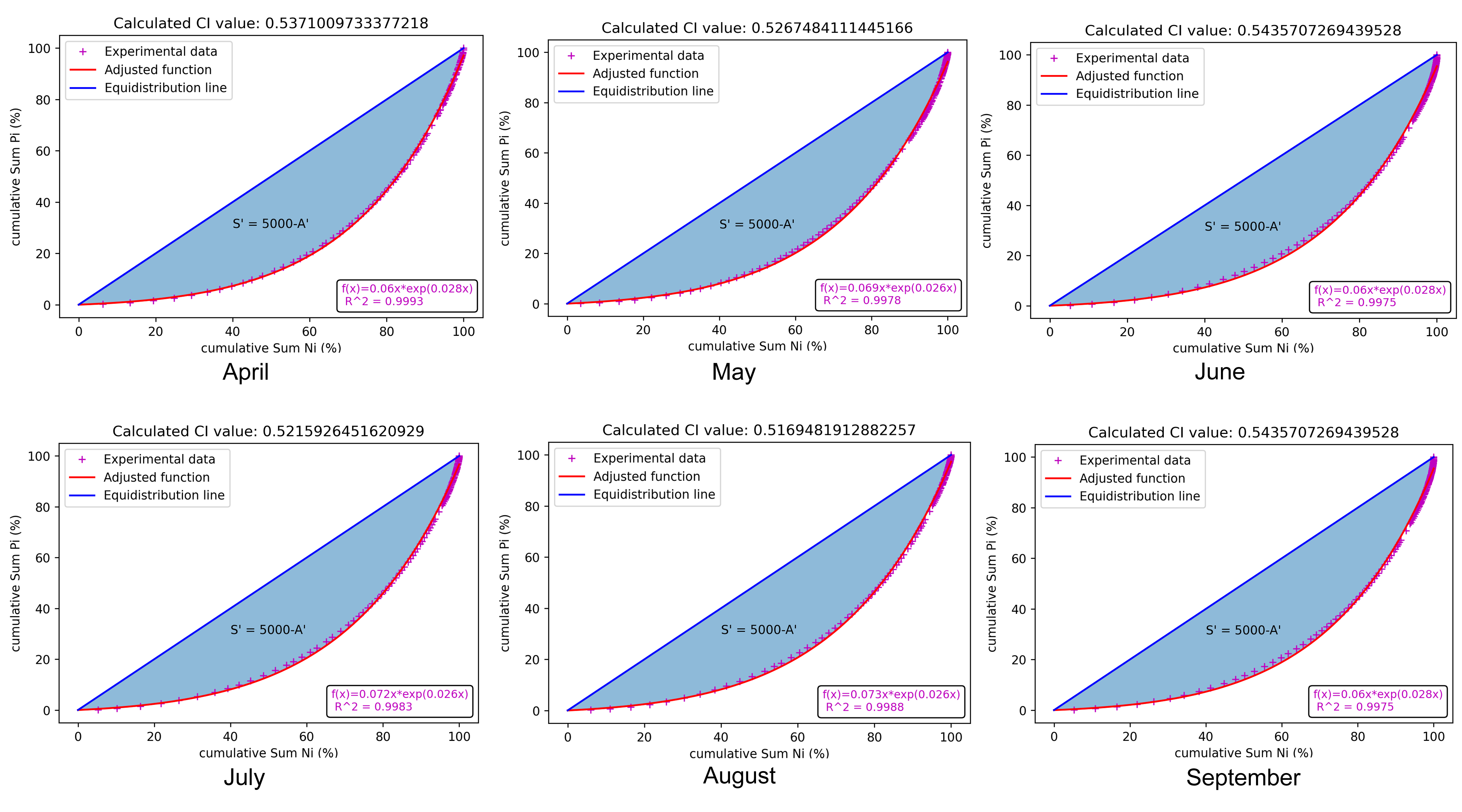
As can be seen, the months with the lowest CI value are April, May, June, July, August, and September (Fig. 2). This means that, for them, less than 65% of rainfall is recorded on 25% of the rainiest days, which means that these are the months with the greatest regularity in the distribution of their rainfall. Considering that the months of May to September belong to the rainy season of the year, this information is very relevant for agricultural and engineering use.
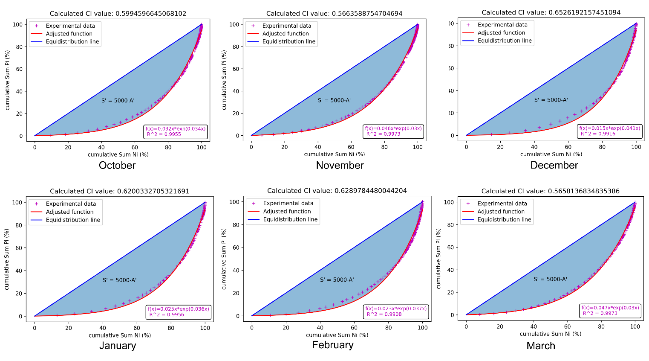
In the case of the months from October to March, the CI values are the highest, meaning that the highest accumulated precipitation is recorded on fewer rainy days (Fig. 3). Although the highest value CIs occur in December, January and February, it is not really too significant for practical purposes since they are months that do not accumulate high historical averages (they belong to the dry season of the year); although very high rainfall has been recorded, as can be seen in Table 1.
In the particular case of the months of June and September, they are the ones with the highest historical average and, in addition, they have registered the maximum precipitation values in 24 hours. Therefore, it is natural to believe that they could be the most worrying for the purposes of agricultural activity, as well as hydraulic and engineering works. However, this analysis obviates the way in which rainfall is typically distributed in these two months, which is characterized by relatively low CI values compared to the rest of the months.
Thus, it can be affirmed that, although these months are characterized by high average historical values of rainfall, they are distributed more evenly than in other months. Therefore, the excess rainfall can be used for its accumulation through the increase in the level of the reservoirs, the recharge of wells, or other activities with a low risk of disasters due to overflows or floods. In this sense, the CI offers a useful criterion to determine which months of the year are the most suitable for these activities safely.
However, in the case of the month of October, when consulting Table 1, it is observed that it registers high historical averages of rainfall, with high standard deviation and the third highest value of rainfall recorded in 24 hours. Considering that, as observed in Table 3, it also has a high CI (0.599), it can be stated that these high volumes of precipitation occur highly concentrated in time (69.47% of the precipitations fall in 25% of the rainy days); that is to say, that few days of the month are those that contribute the greater amount of rain registered.
During this analysis, the saturation conditions in the soil caused by the rains that fell during September, analyzed above, must also be taken into account. For this reason, it can be said that October is potentially the month of greatest care for agricultural activity, as well as hydraulic and engineering works. In this sense, the CI provides important elements for the identification of the most dangerous periods of the year in order to be able to anticipate disasters and take measures in time.
The statistical structure of daily precipitation can be analyzed using concentration curves that relate the accumulated percentages of precipitation contributed by the accumulated percentage of days in which it took place. These curves are adjustable using exponential functions such as equation (4). The CI concentration index, defined on the basis of these curves, makes it possible to evaluate the contrast or concentration of the different daily amounts during certain periods of time and although it has been used in various parts of the world in the literature, there are no references to its use with monthly resolution. In the present work it was shown that the concentration index, calculated monthly, in combination with other statistics, such as the historical average in the same time range, is useful and provides relevant information from the environmental and social point of view; as it allows to know not only how the accumulated in a certain place behave, but also in what way they are distributed over time.
As a result, for the particular case of the Chambas basin, it could be concluded that the month of October is the one of greatest concern, as it presents high accumulated historical records; and also, it has a high CI value (69.47% of rainfall falls on 25% of rainy days).
Benhamrouche, A., Boucherf, D., Hamadache, R., Bendahmane, L., Martín-Vide, J., & J. Teixeira Nery. (2015). Spatial distribution of the daily precipitation concentration index in Algeria. Natural Hazards and Earth System Sciences, 15, 617–625. https://doi.org/https://doi.org/10.5194/nhess-15-617-2015, 2015.
Blanco, E., Brown, O., & García, F. (2021). Relationship between rain and groundwater in the hydrogeological sectors of the South Basin of Ciego de Ávila. INGE CUC, 17(2), 1–8. https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.12
Brooks, C., & Carruthers, N. (1953). Handbooks of statistical methods in meteorology (H. M. S. Office (ed.); Vol. 538). Great Britain Meteorological Office.
Brown, O., Méndez, N., & García, F. (2021). Design of a Windmill for the Water Pumping in a Sprinkle Irrigation System. INGE CUC, 17(2), 0–7. https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.16
Brown, O., & Williams, P. W. (2016). Caudal ecológico del río Chambas en la provincia Ciego de Ávila Ecological flow of Chambas River in Ciego de Avila province. Ingeniería Hidráulica y Ambiental, 37(1), 58–71. https://riha.cujae.edu.cu/index.php/riha/article/view/318
Burgueño, A., Martínez, M. D., Lana, X., & Larrocha, C. S. de. (2005). Statistical distributions of the daily rainfall regime in Catalonia (Northeastern Spain) for the years 1950–2000. International Journal of Climatology, 25(10), 1381–1403. https://doi.org/DOI:10.1002/joc.1197
Burgueño, A., Martínez, M., Serra, C., & Lana, X. (2010). Statistical distributions of daily rainfall regime in europe for the period 1951-2000. Theor. Appl. Climatol., 102, 213–226. https://doi.org/doi:10.1007/s00704-010-0251-5.
Cortesi, N., Gonzalez-Hidalgo, J. C., Brunetti, M., & Martín-Vide, J. (2012). Daily precipitation concentration across Europe 1971-2010. Natural Hazards and Earth System Science, 12(9), 2799–2810. https://doi.org/10.5194/nhess-12-2799-2012
Coscarelli, R., & Caloiero, T. (2012). Analysis of daily and monthly rainfall concentration in Southern Italy (Calabria region). Journal of Hydrology, 416–417, 145–156. https://doi.org/10.1016/j.jhydrol.2011.11.047
INSMET. (2022). El Clima de Cuba. Características generales. http://www.insmet.cu/asp/genesis.asp?TB0=PLANTILLAS&TB1=CLIMAC&TB2=/clima/ClimaCuba.htm
IPCC. (2014). AR5 Climate Change 2014: Impacts, Adaptation, and Vulnerability. https://www.ipcc.ch/report/ar5/wg2/
Jolliffe, I. T., & Hope, P. B. (1996). Representation of daily rainfall distributions using normalized rainfall curves. International Journal of Climatology, 16(10), 1157–1163. https://doi.org/https://doi.org/10.1002/(SICI)1097-0088(199610)16:10<1157::AID-JOC71>3.0.CO;2-R
Li, X., Jiang, F., Li, L., & Wang, G. (2011). Spatial and temporal variability of precipitation concentration index, concentration degree and concentration period in xinjian. Int. J. Climatol., 31, 1679–1693. https://doi.org/doi:10.1002/joc.2181
Martín-Vide, J. (2004). Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8), 959–971. https://doi.org/10.1002/joc.1030
Monjo, R. (2016). Measure of rainfall time structure using the dimensionless n-index. Climate Research, 67(1). https://doi.org/doi:10.3354/cr01359
Monjo, R., & Martín-Vide, J. (2016). Daily precipitation concentration around the world according to several indices. International Journal of Climatology, 36. https://doi.org/10.1002/joc.4596
Myhre, G., Alterskjær, K., Stjern, C. W., Hodnebrog, Marelle, L., Samset, B. H., Sillmann, J., Schaller, N., Fischer, E., Schulz, M., & Stohl, A. (2019). Frequency of extreme precipitation increases extensively with event rareness under global warming. Scientific Reports, 9(1), 1–10. https://doi.org/10.1038/s41598-019-52277-4
Royé, D., & Martín-Vide, J. (2017). Concentration of daily precipitation in the contiguous United States. Atmospheric Research, 196, 237–247. https://doi.org/10.1016/j.atmosres.2017.06.011
Sarricolea, P., & Martín-Vide, J. (2014). Spatial analysis of rainfall daily trends and concentration in Chile. Investigaciones Geográficas, 47. https://doi.org/DOI: 10.5354/0719-5370.2014.32995
Sarricolea, P., & Martín-Vide, J. (2012). Distribución espacial de las precipitaciones diarias en Chile mediante el Índice de Concentración a resolución de 1 mm, entre 1965-2005. VIII Congreso de La Asociación Española de Climatología, 631–639. https://repositorio.aemet.es/bitstream/20.500.11765/8327/1/0061_VIII-2012-P_SARRICOLEA.pdf
Suhaila, J., & Jemain, A. A. (2012). Spatial analysis of daily rainfall intensity and concentration index in peninsular malaysia. Theor. Appl. Climatol., 108, 235–245. https://doi.org/doi:10.1007/s00704-011-0529-2
Zubieta, S. M. (2009). Spatial distribution of a daily precipitation concentration index in central andes of peru, mantaro river valley. TECNIA, 19, 13–22.
Keywords: Concentration index, Monthly rainfall, Daily precipitation, Precipitation indices, Monthly analysis, daily maximum rainfall.
Resumen: La cuenca Chambas, ubicada en la provincia de Ciego de Ávila, Cuba es la principal fuente de suministro para el territorio que atraviesa y ha sido objeto del desarrollo de proyectos hidráulicos. Este estudio examinó la distribución mensual de la precipitación, para determinar los períodos más relevantes desde un punto de vista hidrológico. Para ello, se utilizaron las medidas estadísticas tradicionales en combinación con el índice de concentración diaria de precipitación. Los resultados mostraron que los meses con menor índice de concentración de precipitación son abril, mayo, junio, julio, agosto y septiembre, mientras que de octubre a marzo tuvieron los valores más altos, lo que indica que estos meses acumulan mayor precipitación en menos días de lluvia. Octubre fue identificado como el mes de mayor interés para la actividad agrícola y labores de ingeniería, debido a sus altos promedios históricos de precipitación. Se concluyó que el índice de concentración, calculado mensualmente, en combinación con otras estadísticas, es una herramienta útil y proporciona información relevante.
Palabras clave: Índice de concentración, precipitación mensual, precipitación diaria, índices de precipitación, análisis mensual, máxima precipitación diaria.
1. INTRODUCTION
The detailed temporal structure of precipitation, for example, in a daily resolution, is of vital importance, not only to study climatic factors such as intensity and torrential rains, dry periods and droughts, etc., but also in relation to the soil and ecosystems (erosion, desertification, etc.), management of water resources, flash floods, design of drainage systems, availability and safety of transport systems, urban planning, etc. The study of daily precipitation is particularly relevant in the context of global warming. Several investigations in recent years indicate that there is a statistically significant increasing trend in the frequency and intensity of extreme precipitation events in several parts of the world
(IPCC, 2014
;
AR5 Climate Change 2014: Impacts, Adaptation, and Vulnerability.
https://www.ipcc.ch/report/ar5/wg2/
Myhre et al., 2019)
.
Frequency of extreme precipitation increases extensively with event rareness under global warming. Scientific Reports, 9(1), 1–10.
https://doi.org/10.1038/s41598-019-52277-4
In particular, extreme rainfall events on a daily scale are characterized by durations limited to a small number of days; however, they represent a high percentage of monthly, seasonal and annual precipitation
(Brooks & Carruthers, 1953
;
Handbooks of statistical methods in meteorology (H. M. S. Office (ed.); Vol. 538). Great Britain Meteorological Office.
Jolliffe & Hope, 1996
;
Representation of daily rainfall distributions using normalized rainfall curves. International Journal of Climatology, 16(10), 1157–1163.
https://doi.org/https://doi.org/10.1002/(SICI)1097-0088(199610)16:10<1157::AID-JOC71>3.0.CO;2-R
Martín-Vide, 2004
;
Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8),
959–971. https://doi.org/10.1002/joc.1030
Monjo, 2016)
. Daily rainfall can be considered a discrete process, due to its high number of null values, and can be represented by a negative exponential
distribution
Measure of rainfall time structure using the dimensionless n-index. Climate Research, 67(1).
https://doi.org/doi:10.3354/cr01359
(Brooks & Carruthers, 1953)
. To study the temporal structure of daily precipitation,
Handbooks of statistical methods in meteorology (H. M. S. Office (ed.); Vol. 538). Great Britain Meteorological Office.
Martin-Vide (2004)
developed the Precipitation Concentration Index (CI), which describes and evaluates the percentage contribution of days with precipitation to
the total amount of precipitation. This index has been used successfully in various parts of the world, for example: in Spain
Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8),
959–971. https://doi.org/10.1002/joc.1030
(Burgueño et al., 2005
;
Statistical distributions of the daily rainfall regime in Catalonia (Northeastern Spain) for the years 1950–2000. International Journal of
Climatology, 25(10), 1381–1403. https://doi.org/DOI:10.1002/joc.1197
Martín-Vide, 2004)
; Iran
Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8),
959–971. https://doi.org/10.1002/joc.1030
(Alijan, O’Brien, & Yarnal, 2008)
; China
Spatial analysis of precipitation intensity and concentration in Iran. Theoretical and Applied Climatology, 94, 107–124.
(Li et al., 2011)
; Peru
Spatial and temporal variability of precipitation concentration index, concentration degree and concentration period in Xinjian. Int. J.
Climatol., 31, 1679–1693. https://doi.org/doi:10.1002/joc.2181
(Zubieta, 2009)
; Continental Europe
Spatial distribution of a daily precipitation concentration index in central andes of Peru, Mantaro river valley. TECNIA, 19, 13–22.
(Burgueño et al., 2010
;
Statistical distributions of daily rainfall regime in Europe for the period 1951-2000. Theor. Appl. Climatol., 102, 213–226.
https://doi.org/doi:10.1007/s00704-010-0251-5
Cortesi et al., 2012)
;Peninsular Malaysia
Daily precipitation concentration across Europe 1971-2010. Natural Hazards and Earth System Science, 12(9), 2799–2810.
https://doi.org/10.5194/nhess-12-2799-2012
(Suhaila & Jemain, 2012)
;Southern Italy
Spatial analysis of daily rainfall intensity and concentration index in peninsular Malaysia. Theor. Appl. Climatol., 108, 235–245.
https://doi.org/doi:10.1007/s00704-011-0529-2
(Coscarelli & Caloiero, 2012)
;Chile
Analysis of daily and monthly rainfall concentration in Southern Italy (Calabria region). Journal of Hydrology, 416–417, 145–156.
https://doi.org/10.1016/j.jhydrol.2011.11.047
(Sarricolea & Martín-Vide, 2014,2012)
;Argelia
Spatial analysis of rainfall daily trends and concentration in Chile. Investigaciones Geográficas, 47.
https://doi.org/DOI:10.5354/0719-5370.2014.32995
(Benhamrouche et al., 2015)
;United States
Spatial distribution of the daily precipitation concentration index in Algeria. Natural Hazards and Earth System Sciences, 15, 617–625.
https://doi.org/https://doi.org/10.5194/nhess-15-617-2015
(Royé & Martín-Vide, 2017)
and globally
Concentration of daily precipitation in the contiguous United States. Atmospheric Research, 196, 237–247.
https://doi.org/10.1016/j.atmosres.2017.06.011
(Monjo & Martín-Vide, 2016)
.
Daily precipitation concentration around the world according to several indices. International Journal of Climatology, 36.
https://doi.org/10.1002/joc.4596
In these investigations, the CI has shown to be a reliable estimator of the degree of aggressiveness or rainfall torrentiality, being also explanatory of processes of slope instability, as well as the risks of flooding and drought. However, in all the works carried out, it has been used to characterize the historical behavior of areas from their total records. That is, in no case has a study of this variable been carried out on a monthly basis, even though it is evident that there are differences, significant for various processes, in the way in which rainfall is distributed during the different stages of the year. In the present work a study of the behavior of the daily concentration coefficient at a monthly level is carried out for the Chambas river basin; with the objective of describing the behavior of the accumulation of rainfall in each month. In this way, a useful and practical tool can be obtained to determine which month (s) of the year represent the greatest interest from a hydrological point of view.
2. MATERIALS AND METHODS
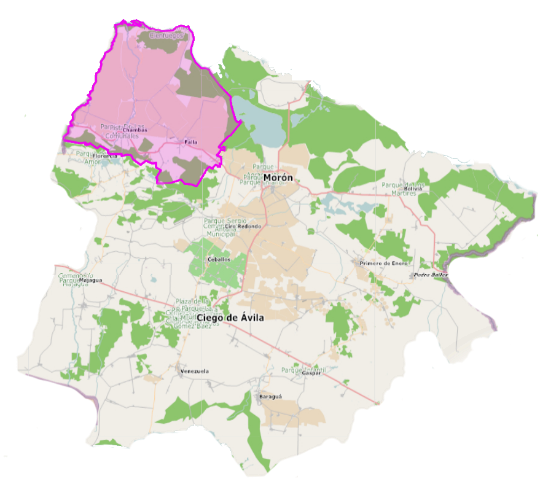
The study was carried out in the Chambas river basin, which covers an area of 333.08 km² of the northwest of the province of Ciego de Ávila, Cuba, as shown in. It is delimited to the north by the Bay of Buena Vista; to the south with the Charco Hondo-Naranjo and Majagua basins; to the east with the Calvario river basin; and to the west with the Jatibonico del Norte river basin. Its importance lies in the fact that it is the main source of supply for the territory it crosses and has been the object of the development of hydraulic projects such as reservoirs, small hydroelectric plants, canals and irrigation systems
(Brown & Williams, 2016)
. The main source of supply for this basin is precipitation. Hence, its characterization in the territory is of great interest.
Caudal ecológico del río Chambas en la provincia Ciego de Ávila Ecological flow of Chambas River in Ciego de Avila province. Ingeniería
Hidráulica y Ambiental, 37(1), 58–71.
https://riha.cujae.edu.cu/index.php/riha/article/view/318

Fig. 1. Location of the Chambas river basin
From the hydrological point of view, a system of dams, micro dams and canals has been built along it with the aim of avoiding floods and supplying water for the development of agriculture, livestock, industry and consumption.
In Cuba, two periods are typically recognized according to their rainfall: one dry, which includes the months from November to April, and the other rainy from May to October
(INSMET, 2022)
. This classification is made based mainly on the historical averages of rainfall in each of the months of the year, and is highly relevant in
several aspects. For instance, it has a decisive influence on agronomic activities, on the allocation of resources for the reinforcement of
infrastructures sensitive to high rainfall accumulations and on the recharge of subterrain aquifers
El Clima de Cuba. Características generales.
http://www.insmet.cu/asp/genesis.asp?TB0=PLANTILLAS&TB1=CLIMAC&TB2=/clima/ClimaCuba.htm
(Blanco et al., 2021)
. In addition, it is essential in the filling of the dams and the future planning of the water it stores, especially as a source of renewable
energy, which together with wind power, is essential in the region
Relationship between rain and groundwater in the hydrogeological sectors of the South Basin of Ciego de Ávila. INGE CUC, 17(2), 1–8.
https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.12
(Brown et al., 2021)
. In the case of the Chambas basin, the average historical precipitation values, the average number of rainy days, the standard deviation of
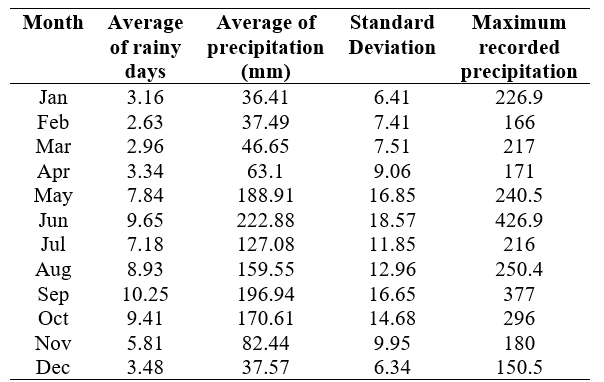
the records and the maximum precipitation recorded for each month can be observed in Table 1, shown below.
Design of a Windmill for the Water Pumping in a Sprinkle Irrigation System. INGE CUC, 17(2), 0–7.
https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.16
Table 1: Average number of rainy days, average precipitation, standard deviation, and maximum recorded precipitation for each month of the year

As can be seen, the behavior of the basin is similar in general terms to the rest of the country with regard to the distribution of its months in the dry and rainy periods. It is under this criterion that decisions of various kinds are generally made; however, the authors of this work consider that it is also important to take into account the way in which rain is distributed on a daily basis; that is, the daily concentration of precipitation, since it is a measure that characterizes the way how the rain falls in a given period.
In terms of the statistical structure of daily precipitation, the distribution of its quantity frequencies is, in general, adjustable by negative exponential distributions, since, when classifying and tabulating the quantities of daily precipitation by longitude, their absolute frequencies decrease exponentially
(Brooks & Carruthers, 1953)
. Therefore, in a finished place and period, most days have very low rainfall while few days have high rainfall. These few days with large
rainfall records can, however, have a considerable weight, that is, represent a notable percentage in the total amount of the determined
place; therefore, they have a decisive effect on the water supply.
Handbooks of statistical methods in meteorology (H. M. S. Office (ed.); Vol. 538). Great Britain Meteorological Office.
In order to evaluate the relative contribution of the rainiest days in a given period, Martín Vide proposed a daily precipitation concentration index (CI)
(Martín-Vide, 2004)
. To obtain it, the author analyzed the different concentration curves that relate the accumulated percentages of precipitation with the
percentage accumulated during the number of days in which it took place. In addition, he took into account the negative exponential curves
that characterize the daily precipitation and the Gini index applied to the Lorentz curves. With this he obtained a tool that allows
evaluating the contrast or concentration of the different daily amounts and their contribution to the accumulated of the region of interest
Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8),
959–971. https://doi.org/10.1002/joc.1030
(Martín-Vide, 2004)
.
Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8),
959–971. https://doi.org/10.1002/joc.1030
2.1 Methodology used to calculate the precipitation concentration index of rainfall
The methodology applied for the analysis of daily precipitation in the historical records of each month is the one proposed by its author, which includes:- Group the precipitations in classes with resolution of 1 mm; starting with [0.1 - 0.99], followed by [1.01 - 1.99], etc., until reaching the interval where the highest daily precipitation record is found.
- Determine the midpoint of each class, called Pm.
- Calculate the magnitude of rainfall for each class, using the following equation. \[ P_i = P_m \cdot n_i \hspace{1cm} (1)\] Where Pi is the daily precipitation in class i (mm); and ni the number of days with rainfall in class i.
- Using the order of the established classes, from least to greatest, calculate the sum of the days with rainfall up to each class; as well as the sum of the precipitation values up to each class.
- Calculate the percentage that represents the sum of the days with rainfall in each class, of the total days with rainfall, according to equation 2. This value will be taken as the abscissa (x values) of the curve used to represent the results. Note that the values of the abscissa will range from 0 to 100. \[ X_j = 100 \cdot \left( \frac{\sum_{i=1}^{j} n_i}{\sum_{j=1}^{N} n_j} \right) \hspace{1cm} (2)\] Where ni is the number of days with rainfall in class i; and N is the total of classes that register days with rainfall.
- Calculate the percentage that represents the sum of rainfall in each class, of the total rainfall, according to equation 3. This value will be taken as the ordinate (y values) of the curve used to represent the results. Note that the ordinate values will range from 0 to 100. \[ Y_j = 100 \cdot \left( \frac{\sum_{i=1}^{j} P_i}{\sum_{j=1}^{N} P_j} \right) \hspace{1cm} (3)\] Where Pi is the number of days with rainfall in class i; and N is the total of classes that register precipitation.
-
Construct the curve from the previously abscissa and ordinate found values that fit the most appropriate mathematical model. In the
present investigation, it was assumed that the values of Xj and Yj were described by a positive exponential relationship, also known as
standard precipitation curve
(Jolliffe & Hope, 1996). This equation is described below. \[Y = a \cdot X \cdot \exp(bX) \hspace{1cm} (4)\] Where a and b are constants, which were estimated using the nonlinear least-square method.Representation of daily rainfall distributions using normalized rainfall curves. International Journal of Climatology, 16(10), 1157–1163. https://doi.org/https://doi.org/10.1002/(SICI)1097-0088(199610)16:10<1157::AID-JOC71>3.0.CO;2-R
- Calculate the area under the curve from the numerical resolution of the definite integral between the limits 0 and 100 (A′). In the present investigation, the Simpson method was used.
- Construct the equidistribution line (origin at 0 and slope 1) on the same graph, which would represent the ideal case where the rains would be uniformly distributed on all the days of the evaluated period.
- Calculate the intermediate area above the curve and under the equidistribution line (S′), which is determined by the difference between the area of the triangle under the equidistribution line (5 000 area units) minus the area under the curve already calculated. \[ \hat{S} = 5000 - \hat{A} \hspace{1cm}(5)\]
- Calculate the CI that results from dividing S' by the area of the triangle under the equidistribution line (5 000 area units). \[ CI = \frac{\hat{S}}{5000} \hspace{1cm}(6)\]
2.2 Data Origin
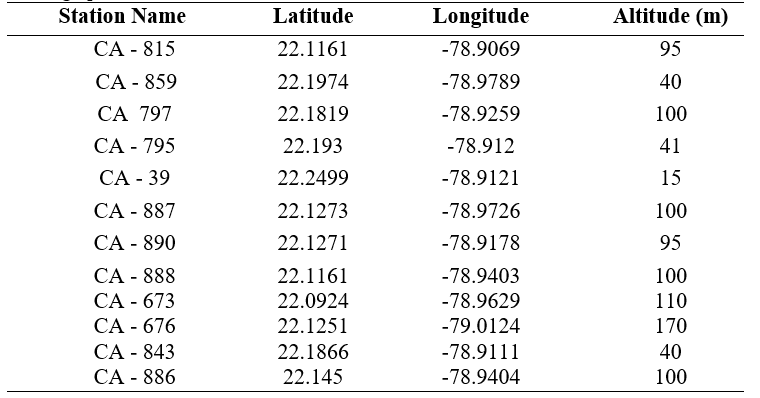
The research analyzed a series of daily rainfall in the period from 1928 to 2013, formed by systematic observations in the rainfall stations CA-676, CA-673, CA-797, CA-886, CA-887, CA-888, CA -815, CA-890, CA-795, CA-843, CA-859 and CA-39, which averaged 37 years of records. In total, 160’284 values were used (13’375 for each month as an average). The geographical coordinates for the stations are shown in Table 2.Table 2: Geographic coordinates for the 12 stations considered, altitude refers to meters above sea level.

To extract the data at the monthly level for the basin, the records of the values contributed by the 12 rain gauges were analyzed as a whole. In this way, for each month the exponential curve of the type of equation (4) was calculated.
3. RESULTS AND DISCUSSION
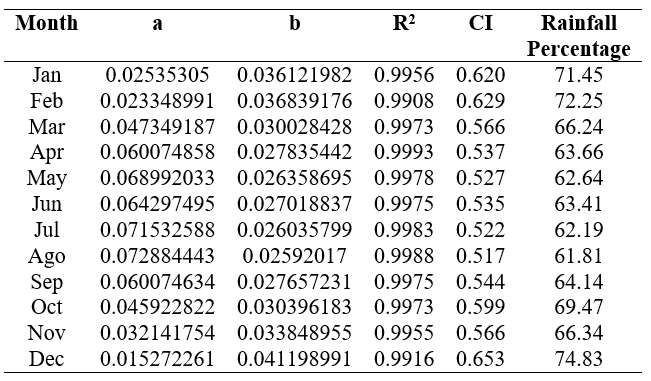
Table 3 shows the estimated values for the constants a and b; the coefficient of determination, which verifies the high level of adjustment of the estimated function for each month (greater than 99% in each case); and the CI values calculated according to equations (5) and (6). Additionally, the percentage of precipitation contributed by the 25% of the rainiest days, that is, the ones with the highest quantity, is shown. This value was obtained using the exponential distribution equation.Table 3:Values of the constants a and b of the exponential curves with the form of equation (4); CI; and the percentage of precipitation contributed by 25% of the rainiest days for each month.

As can be seen, the months with the lowest CI value are April, May, June, July, August, and September (Fig. 2). This means that, for them, less than 65% of rainfall is recorded on 25% of the rainiest days, which means that these are the months with the greatest regularity in the distribution of their rainfall. Considering that the months of May to September belong to the rainy season of the year, this information is very relevant for agricultural and engineering use.

Fig. 2. Precipitation concentration index for months from April to September.
In the case of the months from October to March, the CI values are the highest, meaning that the highest accumulated precipitation is recorded on fewer rainy days (Fig. 3). Although the highest value CIs occur in December, January and February, it is not really too significant for practical purposes since they are months that do not accumulate high historical averages (they belong to the dry season of the year); although very high rainfall has been recorded, as can be seen in Table 1.

Fig. 3. Precipitation concentration index for months from October to March.
In the particular case of the months of June and September, they are the ones with the highest historical average and, in addition, they have registered the maximum precipitation values in 24 hours. Therefore, it is natural to believe that they could be the most worrying for the purposes of agricultural activity, as well as hydraulic and engineering works. However, this analysis obviates the way in which rainfall is typically distributed in these two months, which is characterized by relatively low CI values compared to the rest of the months.
Thus, it can be affirmed that, although these months are characterized by high average historical values of rainfall, they are distributed more evenly than in other months. Therefore, the excess rainfall can be used for its accumulation through the increase in the level of the reservoirs, the recharge of wells, or other activities with a low risk of disasters due to overflows or floods. In this sense, the CI offers a useful criterion to determine which months of the year are the most suitable for these activities safely.
However, in the case of the month of October, when consulting Table 1, it is observed that it registers high historical averages of rainfall, with high standard deviation and the third highest value of rainfall recorded in 24 hours. Considering that, as observed in Table 3, it also has a high CI (0.599), it can be stated that these high volumes of precipitation occur highly concentrated in time (69.47% of the precipitations fall in 25% of the rainy days); that is to say, that few days of the month are those that contribute the greater amount of rain registered.
During this analysis, the saturation conditions in the soil caused by the rains that fell during September, analyzed above, must also be taken into account. For this reason, it can be said that October is potentially the month of greatest care for agricultural activity, as well as hydraulic and engineering works. In this sense, the CI provides important elements for the identification of the most dangerous periods of the year in order to be able to anticipate disasters and take measures in time.
4. CONCLUSIONS
The historical statistical analysis of rainfall in areas of hydrographic interest, such as the Chambas river basin, is not capable of providing all the necessary information on the way in which rainfall is distributed on a daily basis. This generates considerable uncertainty in the average rainfall contributions, which in turn has repercussions of various kinds.The statistical structure of daily precipitation can be analyzed using concentration curves that relate the accumulated percentages of precipitation contributed by the accumulated percentage of days in which it took place. These curves are adjustable using exponential functions such as equation (4). The CI concentration index, defined on the basis of these curves, makes it possible to evaluate the contrast or concentration of the different daily amounts during certain periods of time and although it has been used in various parts of the world in the literature, there are no references to its use with monthly resolution. In the present work it was shown that the concentration index, calculated monthly, in combination with other statistics, such as the historical average in the same time range, is useful and provides relevant information from the environmental and social point of view; as it allows to know not only how the accumulated in a certain place behave, but also in what way they are distributed over time.
As a result, for the particular case of the Chambas basin, it could be concluded that the month of October is the one of greatest concern, as it presents high accumulated historical records; and also, it has a high CI value (69.47% of rainfall falls on 25% of rainy days).
REFERENCES
Alijan, B., O’Brien, J., & Yarnal, B. (2008). Spatial analysis of precipitation intensity and concentration in Iran. Theoretical and Applied Climatology, 94, 107–124.Benhamrouche, A., Boucherf, D., Hamadache, R., Bendahmane, L., Martín-Vide, J., & J. Teixeira Nery. (2015). Spatial distribution of the daily precipitation concentration index in Algeria. Natural Hazards and Earth System Sciences, 15, 617–625. https://doi.org/https://doi.org/10.5194/nhess-15-617-2015, 2015.
Blanco, E., Brown, O., & García, F. (2021). Relationship between rain and groundwater in the hydrogeological sectors of the South Basin of Ciego de Ávila. INGE CUC, 17(2), 1–8. https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.12
Brooks, C., & Carruthers, N. (1953). Handbooks of statistical methods in meteorology (H. M. S. Office (ed.); Vol. 538). Great Britain Meteorological Office.
Brown, O., Méndez, N., & García, F. (2021). Design of a Windmill for the Water Pumping in a Sprinkle Irrigation System. INGE CUC, 17(2), 0–7. https://doi.org/http://doi.org/10.17981/ingecuc.17.2.2021.16
Brown, O., & Williams, P. W. (2016). Caudal ecológico del río Chambas en la provincia Ciego de Ávila Ecological flow of Chambas River in Ciego de Avila province. Ingeniería Hidráulica y Ambiental, 37(1), 58–71. https://riha.cujae.edu.cu/index.php/riha/article/view/318
Burgueño, A., Martínez, M. D., Lana, X., & Larrocha, C. S. de. (2005). Statistical distributions of the daily rainfall regime in Catalonia (Northeastern Spain) for the years 1950–2000. International Journal of Climatology, 25(10), 1381–1403. https://doi.org/DOI:10.1002/joc.1197
Burgueño, A., Martínez, M., Serra, C., & Lana, X. (2010). Statistical distributions of daily rainfall regime in europe for the period 1951-2000. Theor. Appl. Climatol., 102, 213–226. https://doi.org/doi:10.1007/s00704-010-0251-5.
Cortesi, N., Gonzalez-Hidalgo, J. C., Brunetti, M., & Martín-Vide, J. (2012). Daily precipitation concentration across Europe 1971-2010. Natural Hazards and Earth System Science, 12(9), 2799–2810. https://doi.org/10.5194/nhess-12-2799-2012
Coscarelli, R., & Caloiero, T. (2012). Analysis of daily and monthly rainfall concentration in Southern Italy (Calabria region). Journal of Hydrology, 416–417, 145–156. https://doi.org/10.1016/j.jhydrol.2011.11.047
INSMET. (2022). El Clima de Cuba. Características generales. http://www.insmet.cu/asp/genesis.asp?TB0=PLANTILLAS&TB1=CLIMAC&TB2=/clima/ClimaCuba.htm
IPCC. (2014). AR5 Climate Change 2014: Impacts, Adaptation, and Vulnerability. https://www.ipcc.ch/report/ar5/wg2/
Jolliffe, I. T., & Hope, P. B. (1996). Representation of daily rainfall distributions using normalized rainfall curves. International Journal of Climatology, 16(10), 1157–1163. https://doi.org/https://doi.org/10.1002/(SICI)1097-0088(199610)16:10<1157::AID-JOC71>3.0.CO;2-R
Li, X., Jiang, F., Li, L., & Wang, G. (2011). Spatial and temporal variability of precipitation concentration index, concentration degree and concentration period in xinjian. Int. J. Climatol., 31, 1679–1693. https://doi.org/doi:10.1002/joc.2181
Martín-Vide, J. (2004). Spatial distribution of a daily precipitation concentration index in peninsular Spain. International Journal of Climatology, 24(8), 959–971. https://doi.org/10.1002/joc.1030
Monjo, R. (2016). Measure of rainfall time structure using the dimensionless n-index. Climate Research, 67(1). https://doi.org/doi:10.3354/cr01359
Monjo, R., & Martín-Vide, J. (2016). Daily precipitation concentration around the world according to several indices. International Journal of Climatology, 36. https://doi.org/10.1002/joc.4596
Myhre, G., Alterskjær, K., Stjern, C. W., Hodnebrog, Marelle, L., Samset, B. H., Sillmann, J., Schaller, N., Fischer, E., Schulz, M., & Stohl, A. (2019). Frequency of extreme precipitation increases extensively with event rareness under global warming. Scientific Reports, 9(1), 1–10. https://doi.org/10.1038/s41598-019-52277-4
Royé, D., & Martín-Vide, J. (2017). Concentration of daily precipitation in the contiguous United States. Atmospheric Research, 196, 237–247. https://doi.org/10.1016/j.atmosres.2017.06.011
Sarricolea, P., & Martín-Vide, J. (2014). Spatial analysis of rainfall daily trends and concentration in Chile. Investigaciones Geográficas, 47. https://doi.org/DOI: 10.5354/0719-5370.2014.32995
Sarricolea, P., & Martín-Vide, J. (2012). Distribución espacial de las precipitaciones diarias en Chile mediante el Índice de Concentración a resolución de 1 mm, entre 1965-2005. VIII Congreso de La Asociación Española de Climatología, 631–639. https://repositorio.aemet.es/bitstream/20.500.11765/8327/1/0061_VIII-2012-P_SARRICOLEA.pdf
Suhaila, J., & Jemain, A. A. (2012). Spatial analysis of daily rainfall intensity and concentration index in peninsular malaysia. Theor. Appl. Climatol., 108, 235–245. https://doi.org/doi:10.1007/s00704-011-0529-2
Zubieta, S. M. (2009). Spatial distribution of a daily precipitation concentration index in central andes of peru, mantaro river valley. TECNIA, 19, 13–22.