Resumen: En el presente trabajo se modela la producción de hidrógeno en un electrolizador sin membrana para soluciones de KOH, NaCl y NaHCO3 con diferentes concentraciones, empleando la metodología de superficie de respuesta (RSM). Se encontró que el flujo de H2 puede explicarse en función del logaritmo de la potencia entregada y la concentración del electrolito, con un ajuste superior a 95% de acuerdo con los modelos de regresión lineal propuestos a partir de datos obtenidos con un diseño experimental potencio-dinámico para cada tipo de electrolito. Además, se halló un desempeño superior del KOH al 1M, produciendo 22 cm3 estándar por minuto (sccm) a 18W.

Palabras clave: Hidrógeno, Modelamiento, Electrolizador, Superficie de respuesta.

Abstract: In the present work, hydrogen production in a membrane-less electrolizer is modeled for KOH, NaCl and NaHCO3 solutions with different concentrations, using Responce Surface Methodology (RSM). It was found that the H2 flux can be explained as a function of the logarithm of the delivered power and the electrolyte concentration, with a fit better that 95% according to the linear regression models proposed from data obtained with a potentio-dynamic experimental desing for each type of electrolyte. In addition, a superior performance of 1M KOH was found, producing 22 cm3 standard per minute (sccm) at 18W.

Keywords: Hydrogen, Modeling, Electrolyzer, Response Surface.

1. INTRODUCCIÓN

La actual crisis medioambiental ha llevado a gobiernos y empresas a poner en marcha estrategias para mitigar el cambio climático, provocado por la emisión de gases de efecto invernadero derivados del uso de combustibles fósiles en todo el mundo . Una de las soluciones a este problema es la sustitución gradual de estos combustibles por sistemas descentralizados de energías renovables individuales (solar fotovoltaica (FV) y eólica) ( ; ) o sistemas híbridos de energías renovables . En el caso de energías como la solar y la eólica, la luz y la energía cinética se convierten en energía eléctrica, que debe utilizarse inmediatamente. Los sistemas Power-to-Gas en particular son de gran interés para resolver este problema, ya que permiten transformar la energía eléctrica en energía química en forma de gas inflamable de forma similar al gas natural. Los combustibles son vectores energéticos, lo que hace posible transportar este recurso allí donde se necesite y utilizarlo cuando sea necesario. El hidrógeno aparece en este punto como un vector energético para impulsar la implantación de las energías renovables, transformando la energía eléctrica que no se entrega inmediatamente a la red en energía química en forma de hidrógeno gaseoso y oxígeno mediante la electrólisis del agua.

El análisis energético del proceso de electrólisis puede evaluarse termodinámicamente utilizando el cambio de entalpía (ΔH) en la relación de la Ecuación (1).

\[ \Delta H = \Delta G + T \Delta S \hspace{1cm} (1)\]

Donde:
ΔG = Cambio en la energía libre de Gibbs
T = Temperatura
ΔS = Cambio de entropía

Considerando que ΔG es igual a -nEF, donde n es el número de cargas que intervienen en la reacción y F es la constante de Faraday, se puede calcular el potencial mínimo para la descomposición del agua (1.23V) y, en consecuencia, puede hallarse la cantidad mínima de energía necesaria para producir una determinada masa (o volumen) de hidrógeno, que en condiciones estándar del agua sería de 120MJ/KgH2 (LHV), que es la densidad energética gravimétrica más alta en comparación con los combustibles fósiles convencionales y las baterías de litio y plomo-ácido . Experimentalmente, se comprueba que el potencial de la celda necesario para llevar a cabo el proceso de electrólisis cambia obedeciendo a la ecuación de Nernst y variables como el material del electrodo y la concentración del electrolito en el medio acuoso son importantes para determinar el voltaje a aplicar. Además, el punto óptimo de generación de hidrógeno cambiará ya que la densidad de corriente J, además de depender del sobrepotencial, también está ligada al tipo y cantidad de especies químicas en disolución . Este análisis energético requiere conocer la relación de la cantidad de hidrógeno producida a lo largo del tiempo (ccH2/t) con la potencia suministrada (J/t), el tipo de electrolito utilizado y su concentración (M).

En la actualidad, destaca la investigación y posible uso industrial de la producción de hidrógeno con tres tipos de electrolito: líquido, membrana polimérica y membrana cerámica, las dos últimas son membranas sólidas de intercambio iónico específico (H+, OH-, O2-) que requieren principios de funcionamiento más complejos como altas temperaturas (80-1000°C), baja conductividad iónica a través de las membranas (OH-, O2-) y materiales caros (membranas y electrodos) . La electrolisis en electrolito líquido alcalino sigue el principio funcional de las Reacciones de Evolución Hidrógeno y Oxígeno (HER y OER) descritas en las Ecuaciones (2) y (3), en las que el ion encargado de transportar las cargas es el OH-.
\[ 2H_2 O + 4e^- \rightarrow 4OH^- + 2H_2 \hspace{1cm} (2)\] \[ 4OH^- \rightarrow 2H_2O + O_2 + 4e^- \hspace{1cm} (3)\]

Típicamente, los materiales empleados para la fabricación de los electrodos utilizados en estos medios alcalinos son Ni, Co, Mo, Fe (aceros inoxidables) para el ánodo ( ; ) y aleaciones de Ni, Zn, Cu, Cr para el cátodo ( ; ), teniendo aplicaciones comerciales con eficiencias que pueden alcanzar el 70%; aunque los electrolizadores sin membrana tienen desventajas como el medio altamente corrosivo y la pureza de los gases resultantes, las ventajas relacionadas con el coste de los materiales y el mantenimiento, además de la simplicidad de los sistemas son experimentalmente llamativas ( ; ), en particular para la etapa de evaluación de la eficiencia energética y el rendimiento catalítico de los electrodos y su interacción en diferentes medios acuosos.

Debido al gran interés de los procesos de producción de hidrógeno, es necesario modelar el comportamiento en función de las variables más influyentes según el caso. La superficie de respuesta es una metodología de modelamiento con gran éxito en ciencia e ingeniería, ampliamente utilizada en diseño de experimentos para la interpolación de datos mediante el resultado de regresiones lineales utilizando las dos variables más significativas del modelo. El resultado final tiene la forma de la Ecuación (4).
\[ Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 +\beta_3 X_1 X_2 \hspace{1cm} (4)\]

Donde:
Y= Variable dependiente
X1, X2 = Variables independientes
β0 = Intercepto
βn = Coeficientes de las variables independientes y sus interacciones

Para el caso de estudio, Y sería la cantidad de hidrógeno generada y X1, X2 son las variables independientes explicativas más influyentes en el proceso ( ; ; ; ).

2. EXPERIMENTACIÓN

2.1 parámetros del electrolizador

Los experimentos fueron realizados en un electrolizador de electrolito líquido sin membrana, con cavidades individuales para cada electrodo con el fin de realizar una separación de los gases generados. Los materiales para el cátodo y el ánodo fueron cobre electrolítico y acero inoxidable SAE 316L respectivamente, ambos con un área de trabajo de 216cm2 (placas rectangulares de 13.5cm x 8cm sumergidos calibre 0.9mm) y separados 10cm uno del otro, como se evidencia en la Fig 1.

2.2 Variables y diseño experimental

El proceso de modelamiento mediante el RSM se centra en un futuro análisis energético para determinar la eficiencia de un proceso de producción de hidrógeno. Para ello, fue necesario que una de las variables consideradas en la regresión estuviera relacionada con la potencia suministrada al sistema, es decir, QH2(P). Los experimentos se realizaron para 3 tipos diferentes de electrolito (KOH, NaCl, NaHCO3), cada uno con 4 concentraciones diferentes (0,25M, 0,5M, 0,75M y 1M). Se realizaron modelos independientes para cada tipo de electrolito. Dado que la concentración de los iones aumenta la densidad de corriente, ésta se consideró la segunda variable independiente para la superficie de respuesta y, de forma similar a la potencia, el flujo de hidrógeno también puede explicarse en función de la concentración QH2(c).

El diseño experimental contempló un barrido de voltaje con saltos de 500mV/min, midiendo la corriente requerida por el electrolizador en un rango de potencia de 0-20W. Se consideraron los datos para los que había un flujo apreciable de gas a través del sensor (QH2 ≠ 0), como se ve en la Tabla 1. El voltaje y la corriente se relacionan con la potencia según la Ecuación 5.
\[ P = VI \hspace{1cm} (5)\]
Donde:
P = Potencia
V = Voltaje
I = Corriente

El hidrógeno se midió mediante el flujo de salida de la cavidad catódica del electrolizador, utilizando un sensor de flujo másico con principio de transferencia de calor, que no permitía correcciones por variaciones de temperatura y presión. Las unidades de lectura fueron en sccm, que, para el posterior análisis energético, permiten relacionar el caudal de hidrógeno producido (en g/min o cc/min en condiciones estándar) con la potencia aplicada (J/s).

Es importante destacar que las curvas obtenidas para cada concentración no tienen el mismo número de puntos, esto ocurre debido al mencionado aumento de la densidad de corriente en función del potencial aplicado, descrito por la ecuación de Butler-Volmer y el rango de potencias estudiado. El resultado final fue la obtención de datos para la modelización del flujo másico de hidrógeno en función de la potencia y de la concentración QH2 (P,c).

Tabla 1: Diseño experimental propuesto.

Concentration (M)	Power (VxI)	Time (min)
		1	2	3	…	t
0.25	P1	Q1	-	-	…	-
	P2	-	Q2	-	…	-
	P3	-	-	Q3	…	-
	…	…	…	…	…	-
	Pi	-	-	-	-	Qi
0.5	P1	Q1	-	-	…	-
	P2	-	Q2	-	…	-
	P3	-	-	Q3	…	-
	…	…	…	…	…	-
	Pj	-	-	-	-	Qj
0.75	P1	Q1	-	-	…	-
	P2	-	Q2	-	…	-
	P3	-	-	Q3	…	-
	…	…	…	…	…	-
	Pk	-	-	-	-	Qk
1	P1	Q1	-	-	…	-
	P2	-	Q2	-	…	-
	P3	-	-	Q3	…	-
	…	…	…	…	…	-
	Pl	-	-	-	-	Ql

3. RESULTADOS Y DISCUSIÓN

3.1 Análisis de resultados

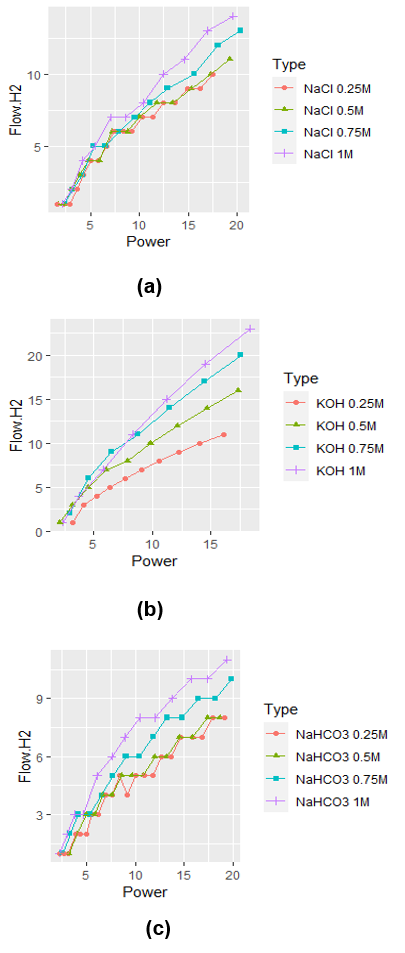
El comportamiento no lineal del flujo frente a la potencia ilustrado en la Fig. 2, muestra una primera aproximación a la relación masa-energía del electrolizador, donde se observa que a medida que aumenta la potencia, el flujo tiende a estabilizarse. Por ello, es correcto suponer que QH2(P) ~ ln(P) para los 3 tipos de electrolito. Del mismo modo, para la concentración, suponer que QH2(c) ~ ln(c) sería correcto para KOH, donde la diferencia entre flujos para el mismo valor de potencia se hace menor a medida que aumenta el valor de concentración. Sin embargo, observando dicho comportamiento para NaCl y NaHCO3, no habría pruebas suficientes para afirmar que esto es cierto. Por eso, a diferencia de la potencia, al tener sólo cuatro valores de concentración, es complejo determinar que esta suposición es válida a simple vista. Esta observación fue analizada en el modelo lineal, postulando que el flujo de hidrógeno podría ser modelado como se indica en la Ecuación (6).
\[ Q_{(H_2)} = \beta_0 + \beta_1 \ln(P) + \beta_2 \ln(c) + \beta_3 \ln(P)\ln(c) \hspace{1cm} (6)\]


Los rangos de voltaje aplicados fueron de 2-9,5V para KOH, 3-13,5V para NaCl y 5-17,5V para NaHCO3 y sus respectivos rangos de densidad de corriente de 2-14mA/cm2, 0,5-11mA/cm2 y 0,5-8mA/cm2. Se puede confirmar que la mayor cantidad de hidrógeno se produce empleando como electrolito una solución 1M de KOH, alcanzando una producción de 22sccm a 18W (~6V), seguido de NaCl con 18sccm a 20W (~8V) y finalmente NaHCO3 con 11sccm a 20W (~11.5V).

3.2 Análisis estadístico

En primer lugar, se realizó un ANOVA que mostró que al menos un par de medias en el conjunto de datos son significativamente diferentes entre sí para los tres tipos de electrolito, como se evidencia en la Tabla 2.

Tabla 2: Resultados del análisis de varianza por tipo de electrolito.

Electrolyte	Variable	Df	Sum Sq	Mean Sq	F value	P-value
KOH	ln(P)	1	845.0	845.0	379.69	< 2x10-16
	ln(c)	1	154.1	154.1	69.25	2.74x10-9
	Residuals	30	66.8	2.2	-	-
NaCl	ln(P)	1	611.9	611.9	813.99	< 2x10-16
	ln(c)	1	15.2	15.2	20.23	3.88x10-5
	Residuals	52	39.1	0.8	-	-
NaHCO3	ln(P)	1	390.7	390.7	888.36	< 2x10-16
	ln(c)	1	33.4	33.4	75.87	2.66x10-12
	Residuals	61	26.8	0.4	-	-

En los tres modelos lineales se incluyeron las variables involucradas en la Ecuación (6), acorde al comportamiento de los resultados experimentales. De acuerdo con el p-valor, para cada uno de los tratamientos y los interceptos de las regresiones existe significancia (valor-p < α) excepto para la variable ln(c) en el caso del NaHCO3. A pesar de ello, dado que el término de interacción es significativo, esta variable no puede excluirse del modelo.

Los coeficientes muestran que ln(P) tiene el mayor efecto sobre el flujo de gas para los 3 modelos y es superior para KOH como se observa en los resultados experimentales. Los efectos de ln(c) son menores, principalmente para NaCl y NaHCO3 donde el aumento de concentración evidencia diferencias de 1-4 sccm en contraste con KOH donde para el mismo valor de potencia hay diferencias de hasta 10 sccm.

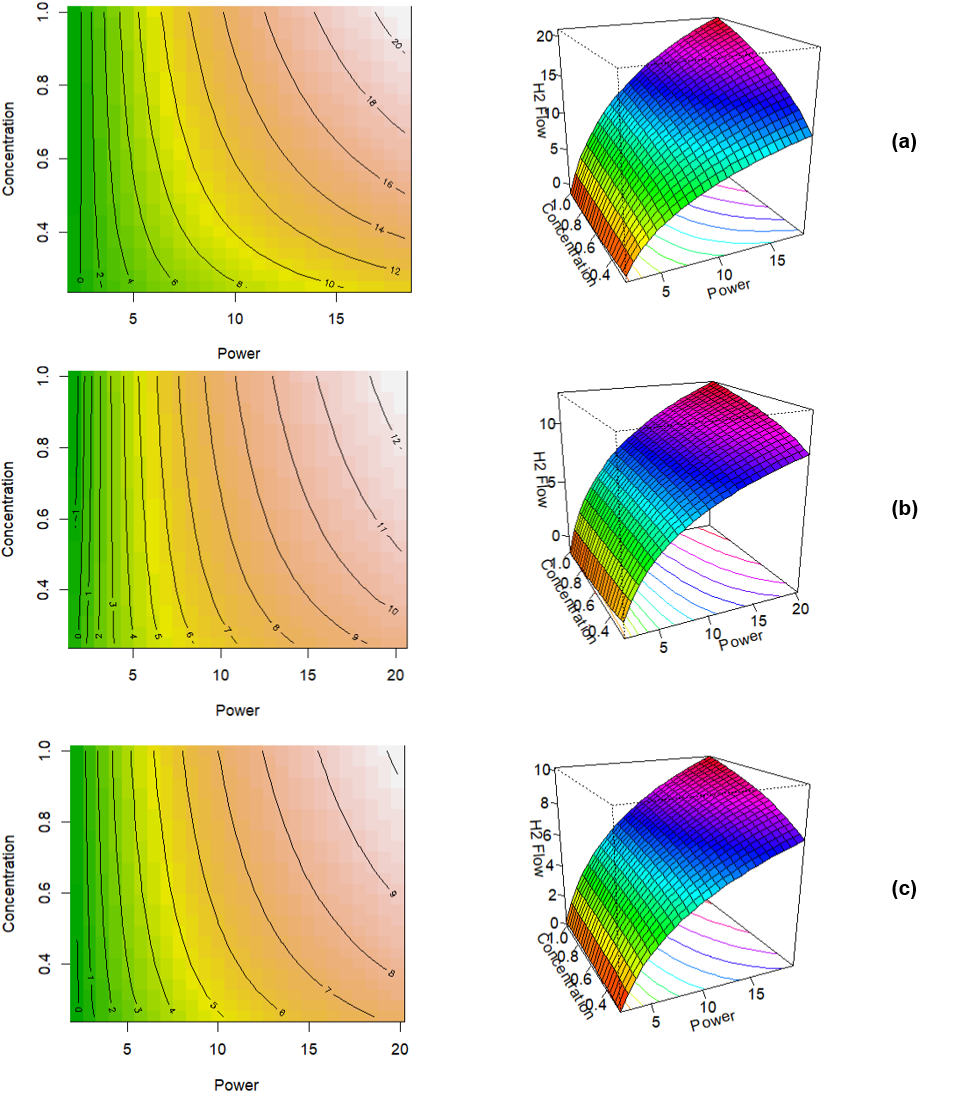
El término de interacción es significativo para los 3 modelos indicando que existe una fuerte dependencia entre la relación concentración-potencia y la producción de hidrógeno. Los modelos obtenidos se muestran en las Ecuaciones (6), (7) y (8), que obedecen a la forma de la Ecuación (4) propuesta inicialmente. Los modelos tienen ajustes de 0,97, 0,96 y 0,95 evidenciados en la Tabla 3, lo que indica una gran similitud con los resultados experimentales que pueden contrastarse con las superficies de respuesta de la Fig. 5.
\[ Q_{(H_2 KOH)}(P,c) = -9.05 + 10.28 \ln(P) - 3.17 \ln(c) + 3.54 \ln(P) \ln(c) \hspace{1cm} (7)\] \[ Q_{(H_2 NaCl)}(P,c) = -4.31 + 5.59 \ln(P) - 1.51 \ln(c) + 1.25 \ln(P) \ln(c) \hspace{1cm} (8)\] \[ Q_{(H_2 NaHCO_3)}(P,c) = -3.54 + 4.58 \ln(P) - 0.47 \ln(c) + 0.86 \ln(P) \ln(c) \hspace{1cm} (9)\]

Tabla3: Resultados de las regresiones lineales por tipo de electrolito.

Electrolyte	Variable	Coeff. Est	Est. Error	t value	P-value	Multiple R2	Adjusted R2
KOH	Intercept	-9.05	0.90	-10.00	6.47x10-11
	ln(P)	10.28	0.42	24.20	< 2x10-16
	Ln(c)	-3.17	1.20	-2.65	0.01	0.97	0.97
	ln(P)*ln(c)	3.54	0.56	6.29	7.27x10-7
NaCl	Intercept	-4.31	0.51	-8.52	2.22x10-11
	ln(P)	5.59	0.24	23.77	< 2x10-16
	Ln(c)	-1.51	0.57	-2.65	0.01	0.96	0.96
	ln(P)*ln(c)	1.25	0.27	4.63	2.57x10-5
NaHCO3	Intercept	-3.54	0.41	-8.58	5.03x10-12
	ln(P)	4.58	0.19	24.47	< 2x10-16
	Ln(c)	-0.47	0.46	-1.02	0.31	0.95	0.95
	ln(P)*ln(c)	0.86	0.21	4.07	1.39x10-4

4. CONCLUSIONES

Los datos obtenidos a partir del diseño experimental propuesto permitieron postular una transformación logarítmica para los valores iniciales de potencia y concentración con el fin de obtener una relación lineal con respecto al flujo de hidrógeno. Estadísticamente, se confirmó que los modelos de regresión con dichas transformaciones se ajustan a los datos experimentales en un 97% para KOH, 96% para NaCl y 95% para NaHCO3, siendo una modelización fiable para un análisis de eficiencia energética.

Los mayores flujos de hidrógeno se alcanzan utilizando soluciones 1M de cada electrolito; en primer lugar, KOH (22sccm a 18W) seguido de NaCl (18 sccm a 20W) y finalmente NaHCO3 (11sccm a 20W). Del mismo modo, el flujo aumenta al aumentar la potencia del electrolizador, de acuerdo con las ecuaciones (6), (7) y (8).

RECONOCIMIENTO

A la Universidad de Antioquia y al grupo de investigación TESLA.

REFERENCIAS

Lamb, W. F., Wiedmann, T., Pongratz, J., Andrew, R., Crippa, M., Olivier, J. G., ... & Minx, J. (2021). A review of trends and drivers of greenhouse gas emissions by sector from 1990 to 2018. Environmental research letters, 16(7), 073005.

Victoria, M., Haegel, N., Peters, I. M., Sinton, R., Jäger-Waldau, A., del Canizo, C., ... & Smets, A. (2021). Solar photovoltaics is ready to power a sustainable future. Joule, 5(5), 1041-1056.

Olabi, A. G., Wilberforce, T., Elsaid, K., Salameh, T., Sayed, E. T., Husain, K. S., & Abdelkareem, M. A. (2021). Selection guidelines for wind energy technologies. Energies, 14(11), 3244.

Mazzeo, D., Matera, N., De Luca, P., Baglivo, C., Congedo, P. M., & Oliveti, G. (2021). A literature review and statistical analysis of photovoltaic-wind hybrid renewable system research by considering the most relevant 550 articles: An upgradable matrix literature database. Journal of Cleaner Production, 295, 126070.

Ozturk, M., & Dincer, I. (2021). A comprehensive review on power-to-gas with hydrogen options for cleaner applications. International Journal of Hydrogen Energy, 46(62), 31511-31522.

Møller, K. T., Jensen, T. R., Akiba, E., & Li, H. W. (2017). Hydrogen-A sustainable energy carrier. Progress in Natural Science: Materials International, 27(1), 34-40.

Li, J., Liu, W., & Qi, W. (2021). Hydrogen production technology by electrolysis of water and its application in renewable energy consumption. In E3S Web of Conferences (Vol. 236, p. 02001). EDP Sciences.

Ezzahra Chakik, F., Kaddami, M., & Mikou, M. (2017). Effect of operating parameters on hydrogen production by electrolysis of water. international journal of hydrogen energy, 42(40), 25550-25557.

Chi, J., & Yu, H. (2018). Water electrolysis based on renewable energy for hydrogen production. Chinese Journal of Catalysis, 39(3), 390-394.

Wei, J., Zhou, M., Long, A., Xue, Y., Liao, H., Wei, C., & Xu, Z. J. (2018). Heterostructured electrocatalysts for hydrogen evolution reaction under alkaline conditions. Nano-micro letters, 10(4), 1-15.

Manzotti, A., Quattrocchi, E., Curcio, A., Kwok, S. C., Santarelli, M., & Ciucci, F. (2022). Membraneless electrolyzers for the production of low-cost, high-purity green hydrogen: A techno-economic analysis. Energy Conversion and Management, 254, 115156.

Esposito, D. V. (2017). Membraneless electrolyzers for low-cost hydrogen production in a renewable energy future. Joule, 1(4), 651-658.

Garimella, S., Vimal, A., Merugu, R., & Kumar, A. (2019). Optimization for enhanced hydrogen production from Rhodobacter sphaeroides using response surface methodology. SN Applied Sciences, 1(2), 1-8.

Chee, M. K., Ng, B. J., Chew, Y. H., Chang, W. S., & Chai, S. P. (2022). Photocatalytic Hydrogen Evolution from Artificial Seawater Splitting over Amorphous Carbon Nitride: Optimization and Process Parameters Study via Response Surface Modeling. Materials, 15(14), 4894.

Özgür, C., & Mert, M. E. (2022). Prediction and optimization of the process of generating green hydrogen by electrocatalysis: A study using response surface methodology. Fuel, 330, 125610.

Naseer, M. N., Zaidi, A. A., Khan, H., Kumar, S., Owais, M. T. B., Abdul Wahab, Y., & Alrobei, H. (2021). Statistical modeling and performance optimization of a two-chamber microbial fuel cell by response surface methodology. Catalysts, 11(10), 1202.